Question

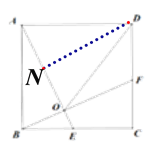
【题目】（本题满分14分）如图，在正方形ABCD中，AB=5.点E为BC边上一点（不与点B重合），点F为CD边上一点，线段AE、BF相交于点O,其中AE=BF.

(1)求证：AE⊥BF；

(2)若OA-OB=1，求OA的长及四边形OECF的面积；

(3)连接OD,若△AOD是以AD为腰的等腰三角形，求AE的长.

Answer 1

【答案】（1）证△ABE≌△BCF（2）OA=4，6

（3）

【解析】在△ABE和△BCF中

∵AB=BC,AE=BF

∴△ABE≌△BCF(HL),

∴∠BAE=∠CBF.

∵∠BAE+∠AEB=90°,

∴∠CBF+∠AEB=90°,

∴AE⊥BF.

设OA=x,则OB=x-1.

由勾股定理得

解之得

， （舍去）

.

,

,, .

,

,

,

（3）由题意知AD=OD.作DN⊥AE于点N.

在△ABO和△DAN中

∵∠AOB=∠AND, ∠DAN=∠ABO,AD=AB

∴△ABO≌△DAN（AAS）

∴AN=ON=OB

设AN=ON=OB=x，则OA=2x.

由勾股定理得

解之得

.

∵△ABO∽△AEB

, ， .