
如图1,点P为∠MON的平分线上一点,以P为顶点的角的两边分别与射线OM,ON交于A,B两点,如果∠APB绕点P旋转时始终满足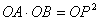 ,我们就把∠APB叫做∠MON的智慧角.
,我们就把∠APB叫做∠MON的智慧角.
(1)如图2,已知∠MON=90°,点P为∠MON的平分线上一点,以点P为顶点的角的两边分别与射线OM,ON交于A,B两点,且∠APB=135°. 求证:∠APB是∠MON的智慧角;
(2)如图1,已知∠MON=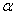 (0°<
(0°<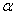 <90°),OP=2,若∠APB是∠MON的智慧角,连结AB,用含
<90°),OP=2,若∠APB是∠MON的智慧角,连结AB,用含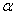 的式子分别表示∠APB的度数和△AOB的面积;
的式子分别表示∠APB的度数和△AOB的面积;
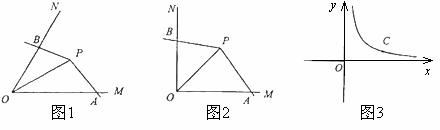
(3)如图3,C是函数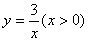 图象上的一个动点,过点C的直线CD分别交
图象上的一个动点,过点C的直线CD分别交 轴和
轴和 轴于点A,B两点,且满足BC=2CA,请求出∠AOB的智慧角∠APB的顶点P的坐标.
轴于点A,B两点,且满足BC=2CA,请求出∠AOB的智慧角∠APB的顶点P的坐标.
解:(1)证明:∵∠MON=90°,点P为∠MON的平分线上一点,
∴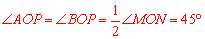 .
.
∵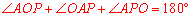 ,∴
,∴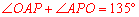 .
.
∵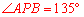 ,∴
,∴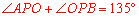 .∴
.∴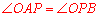 .
.
∴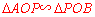 .∴
.∴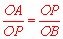 ,即
,即 .
.
 ∴∠APB是∠MON的智慧角.
∴∠APB是∠MON的智慧角.
(2)∵∠APB是∠MON的智慧角,
∴ ,即
,即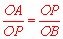 .
.
∵点P为∠MON的平分线上一点,
∴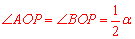 .
.
∴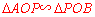 .∴
.∴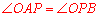 .
.
∴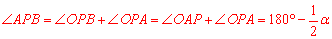 .
.
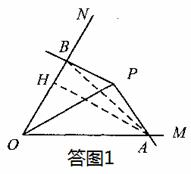
如答图1,过点A作AH⊥OB于点H,
∴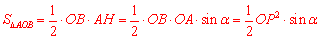 .
.
∵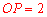 ,∴
,∴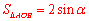 .
.
(3)设点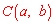 ,则
,则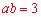 .如答图,过C点作CH⊥OA于点H.
.如答图,过C点作CH⊥OA于点H.
i)当点B在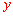 轴的正半轴时,
轴的正半轴时,
如答图2,当点A在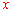 轴的负半轴时,
轴的负半轴时,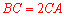 不可能.
不可能.
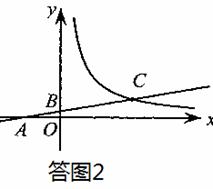
如答图3,当点A在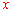 轴的正半轴时,
轴的正半轴时,
∵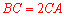 ,∴
,∴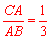 .
.
∵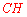 ∥
∥ ,∴
,∴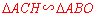 .∴
.∴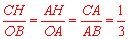 .∴
.∴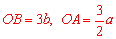 .
.
∴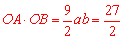 .
.
∵∠APB是∠AOB的智慧角,∴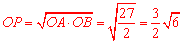 .
.
∵∠AOB=90°,OP平分∠AOB,∴点P的坐标为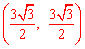 .
.
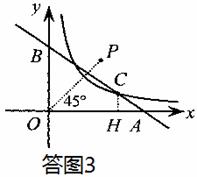
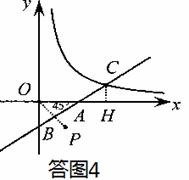
ii)当点B在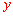 轴的负半轴时,如答图4
轴的负半轴时,如答图4
∵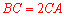 ,∴
,∴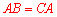 .
.
∵∠AOB=∠AHC=90°,∠BAO=∠CAH,∴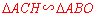 .
.
∴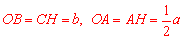 .∴
.∴ .
.
∵∠APB是∠AOB的智慧角,∴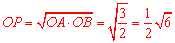 .
.
∵∠AOB=90°,OP平分∠AOB,∴点P的坐标为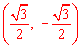 .
.
综上所述,点P的坐标为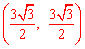 或
或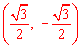 .
.
【考点】新定义和阅读理解型问题;单动点和旋转问题;相似三角形的判定和性质;锐角三角函数定义;反比例函数的性质;曲线上点的坐标与方程的关系;分类思想的应用.
【分析】(1)通过证明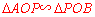 ,即可得到
,即可得到 ,从而证得∠APB是∠MON的智慧角.
,从而证得∠APB是∠MON的智慧角.
(2)根据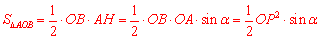 得出结果.
得出结果.
(3)分点B在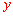 轴的正半轴,点B在
轴的正半轴,点B在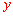 轴的负半轴两种情况讨论.
轴的负半轴两种情况讨论.


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
某厂制作甲、乙两种环保包装盒。已知同样用6m的材料制成甲盒的个数比制成乙盒的个数少2个,且制成一个甲盒比制作一个乙盒需要多用20%的材料。
(1)求制作每个甲盒、乙盒各用多少材料?
(2)如果制作甲、乙两种包装盒3000个,且甲盒的数量不少于乙盒数量的2倍,那么请写出所需材料总长度 与甲盒数量
与甲盒数量 之间的函数关系式,并求出最少需要多少米材料。
之间的函数关系式,并求出最少需要多少米材料。
查看答案和解析>>
科目:初中数学 来源: 题型:
一个不透明的布袋里装有2个白球,1个黑球和若干个红球,它们除颜色外其余都相同,从中任意摸出1个球,是白球的概率为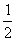 .
.
(1)布袋里红球有多少个?
(2)先从布袋中摸出1个球后不放回,再摸出1个球,请用列表或画树状图等方法求出两次摸到的球都是白球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
在比例尺为1:8000的南京市城区地图上,太平南路的长度约为25 cm,它的实际长度约为 ( )
A. 320 cm B.320m C.2000 cm D.2000 m
查看答案和解析>>
科目:初中数学 来源: 题型:
已知A、B两地的实际距离是300 km,量得两地在地图上的距离是5 cm.
(1)该地图的比例尺是______________.
(2)若在该地图上量得A、C两地间的距离是16 cm,则A、C两地间的实际距离是_______km.
查看答案和解析>>
科目:初中数学 来源: 题型:
在△ABC中,AB=AC,∠A=60°,点D是线段BC的中点,∠EDF=120°,DE与线段AB相交于点E,DF与线段AC(或AC的延长线)相交于点F.
(1)如图1,若DF⊥AC,垂足为F,AB=4,求BE的长;
(2)如图2,将(1)中的∠EDF绕点D顺时针旋转一定的角度,DF扔与线段AC相交于点F.求证: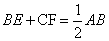 ;
;
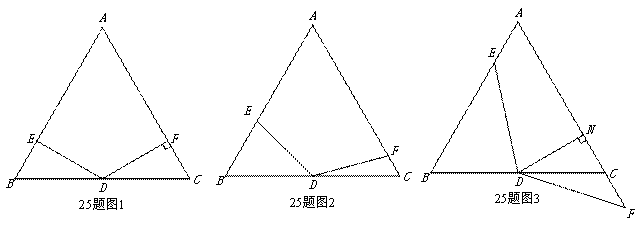
(3)如图3,将(2)中的∠EDF继续绕点D顺时针旋转一定的角度,使DF与线段AC的延长线交与点F,作DN⊥AC于点N,若DN=FN,求证: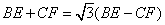 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com