
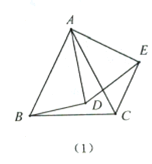
【题目】我们定义:如果两个等腰三角形的顶角相等,且项角的顶点互相重合,则称此图形为“手拉手全等模型”.因为顶点相连的四条边,形象的可以看作两双手,所以通常称为“手拉手模型”.例如,如(1),![]() 与
与![]() 都是等腰三角形,其中
都是等腰三角形,其中![]() ,则△ABD≌△ACE(SAS).
,则△ABD≌△ACE(SAS).
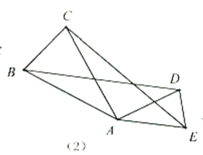
(1)熟悉模型:如(2),已知![]() 与
与![]() 都是等腰三角形,AB=AC,AD=AE,且
都是等腰三角形,AB=AC,AD=AE,且![]() ,求证:
,求证:![]() ;
;
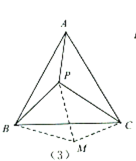
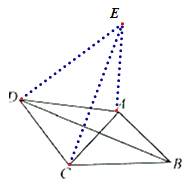
(2)运用模型:如(3),![]() 为等边
为等边![]() 内一点,且
内一点,且![]() ,求
,求![]() 的度数.小明在解决此问题时,根据前面的“手拉手全等模型”,以
的度数.小明在解决此问题时,根据前面的“手拉手全等模型”,以![]() 为边构造等边
为边构造等边![]() ,这样就有两个等边三角形共顶点
,这样就有两个等边三角形共顶点![]() ,然后连结
,然后连结![]() ,通过转化的思想求出了
,通过转化的思想求出了![]() 的度数,则
的度数,则![]() 的度数为 度;
的度数为 度;
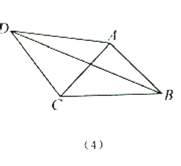
(3)深化模型:如(4),在四边形![]() 中,AD=4,CD=3,∠ABC=∠ACB=∠ADC=45°,求
中,AD=4,CD=3,∠ABC=∠ACB=∠ADC=45°,求![]() 的长.
的长.
【答案】(1)见解析;(2)150°;(3)![]()
【解析】
(1)根据“SAS”证明△ABD≌△ACE即可;
(2)根据小明的构造方法,通过证明△BAP≌△BMC,可证∠BPA=∠BMC,AP=CM,根据勾股定理的逆定理得到∠PMC=90°,于是得到结论;
(3)根据已知可得△ABC是等腰直角三角形,所以将△ADB绕点A逆时针旋转90°,得到△ACE,则BD=CE,证明△DCE是直角三角形,再利用勾股定理可求CE值.
(1)∵![]() ,
,
∴![]() ,
,
在△ABD和△ACE中,
∵![]() ,
,
![]() ,
,
AD=AE,
∴△ABD≌△ACE,
∴![]() ;
;
(2)由小明的构造方法可得,
BP=BM=PM,∠PBM=∠PMB=60°,
∴∠ABP=∠CBM,
又∵AB=BC,
∴△BAP≌△BMC,
∴∠BPA=∠BMC,AP=CM,
∵![]() ,
,
∴![]() ,
,
设CM=3x,PM=4x,PC=5x,
∵(5x)2=(3x)2+(4x)2,
∴PC2=CM2+PM2,
∴△PCM是直角三角形,
∴∠PMC=90°,
∴∠BPA=∠BMC=60°+90°=150°;
(3)∵∠ACB=∠ABC=45°,
∴∠BAC=90°,且AC=AB.
将△ADB绕点A顺时针旋转90°,得到△ACE,
∴AD=AE,∠DAE=90°,BD=CE.
∴∠EDA=45°,DE=![]() AD=4
AD=4![]() .
.
∵∠ADC=45°,
∴∠EDC=45°+45°=90°.
在Rt△DCE中,利用勾股定理可得,
CE= ![]() ,
,
∴BD=CE=![]() .
.


科目:初中数学 来源: 题型:
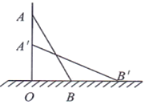
【题目】如图,一架云梯AB长25分米,斜靠在一面墙上,梯子底端B离墙7分米.
(1)这个梯子的顶端A距地面有多高?
(2)如果梯子顶端下滑了4分米,那么梯子的底端在水平方向滑动了多少分米?
查看答案和解析>>
科目:初中数学 来源: 题型:
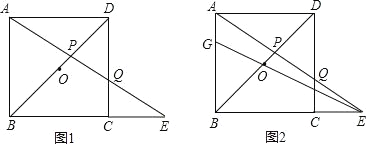
【题目】如图1,ABCD是边长为1的正方形,O是正方形的中心,Q是边CD上一个动点(点Q不与点C、D重合),直线AQ与BC的延长线交于点E,AE交BD于点P.设DQ=x.
(1)填空:当![]() 时,
时,![]() 的值为 ;
的值为 ;
(2)如图2,直线EO交AB于点G,若BG=y,求y关于x之间的函数关系式;
(3)在第(2)小题的条件下,是否存在点Q,使得PG∥BC?若存在,求x的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程mx2+(3m+1)x+3=0.
(1)求证:该方程有两个实数根;
(2)如果抛物线y=mx2+(3m+1)x+3与x轴交于A、B两个整数点(点A在点B左侧),且m为正整数,求此抛物线的表达式;
(3)在(2)的条件下,抛物线y=mx2+(3m+1)x+3与y轴交于点C,点B关于y轴的对称点为D,设此抛物线在﹣3≤x≤﹣![]() 之间的部分为图象G,如果图象G向右平移n(n>0)个单位长度后与直线CD有公共点,求n的取值范围.
之间的部分为图象G,如果图象G向右平移n(n>0)个单位长度后与直线CD有公共点,求n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下表:
x | 2.1 | 2.2 | 2.3 | 2.4 | 2.5 | 2.6 | 2.7 | 2.8 | 2.9 |
y=x2﹣2x﹣2 | ﹣1.79 | ﹣1.56 | ﹣1.31 | ﹣1.04 | ﹣0.75 | ﹣0.44 | ﹣0.11 | 0.24 | 0.61 |
则一元二次方程x2﹣2x﹣2=0在精确到0.1时一个近似根是 ________ ,利用抛物线的对称性,可推知该方程的另一个近似根是________ .
查看答案和解析>>
科目:初中数学 来源: 题型:
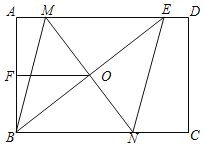
【题目】如图,在矩形ABCD中,E是AD上一点,MN垂直平分BE,分别交AD,BE,BC于点M,O,N,连接BM,EN
(1)求证:四边形BMEN是菱形.
(2)若AE=8,F为AB的中点,BF+OB=8,求MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,D,E 分别是 AB,BC 上的点,且 DE∥AC,若 S△BDE:S△CDE=1:3,则S△DEB: S△ADC=( )

A. 1:5 B. 1:9 C. 1:10 D. 1:12
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com