
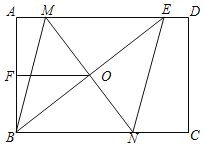
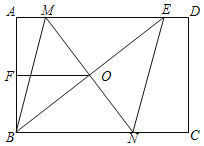
【题目】如图,在矩形ABCD中,E是AD上一点,MN垂直平分BE,分别交AD,BE,BC于点M,O,N,连接BM,EN
(1)求证:四边形BMEN是菱形.
(2)若AE=8,F为AB的中点,BF+OB=8,求MN的长.
【答案】(1)证明见解析;(2)MN=![]() .
.
【解析】
(1)先根据线段垂直平分线的性质证明MB=ME,由ASA证明△BON≌△EOM,得出ME=NB,证出四边形BMEN是平行四边形,再根据菱形的判定即可得出结论;
(2)根据已知条件得到AB+BE=2BF+2OB=16,设AB=x,则BE=16﹣x,根据勾股定理得到x=6,求得BE=16﹣x=10,OB=![]() BE=5,设ME=y,则AM=8﹣y,BM=ME=y,根据勾股定理即可得到结论.
BE=5,设ME=y,则AM=8﹣y,BM=ME=y,根据勾股定理即可得到结论.
(1)证明:∵MN垂直平分BE,
∴MB=ME,OB=OE,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠MEO=∠NBO,
在△BON与△EOM中,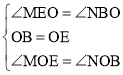 ,
,
∴△BON≌△EOM(ASA),
∴ME=NB,
又∵AD∥BC,
∴四边形BMEN是平行四边形,
又∵MB=ME,
∴四边形BMEN是菱形;
(2)解:∵O,F分别为MN,AB的中点,
∴OF∥AD,
∴∠OFB=∠EAB=90°,
∵BF+OB=8,
∴AB+BE=2BF+2OB=16,
设AB=x,则BE=16﹣x,
在Rt△ABE中,82+x2=(16﹣x)2,
解得x=6,
∴BE=16﹣x=10,
∴OB=![]() BE=5,
BE=5,
设ME=y,则AM=8﹣y,BM=ME=y,
在Rt△ABM中,62+(8﹣y)2=y2,
解得y=![]() ,
,
在Rt△BOM中,MO=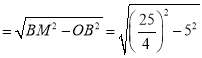 =
=![]() ,
,
∴MN=2MO=![]() .
.


科目:初中数学 来源: 题型:
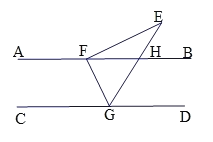
【题目】如图,AB// CD,Rt△EFG的顶点F,G分别落在直线AB,CD上,GE交AB于点H,∠EFG=90°,∠E=32°.
(1)∠FGE= °
(2)若GE平分∠FGD,求∠EFB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
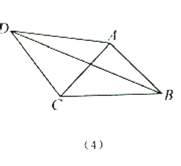
【题目】我们定义:如果两个等腰三角形的顶角相等,且项角的顶点互相重合,则称此图形为“手拉手全等模型”.因为顶点相连的四条边,形象的可以看作两双手,所以通常称为“手拉手模型”.例如,如(1),![]() 与
与![]() 都是等腰三角形,其中
都是等腰三角形,其中![]() ,则△ABD≌△ACE(SAS).
,则△ABD≌△ACE(SAS).
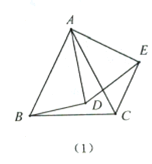
(1)熟悉模型:如(2),已知![]() 与
与![]() 都是等腰三角形,AB=AC,AD=AE,且
都是等腰三角形,AB=AC,AD=AE,且![]() ,求证:
,求证:![]() ;
;
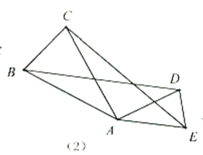
(2)运用模型:如(3),![]() 为等边
为等边![]() 内一点,且
内一点,且![]() ,求
,求![]() 的度数.小明在解决此问题时,根据前面的“手拉手全等模型”,以
的度数.小明在解决此问题时,根据前面的“手拉手全等模型”,以![]() 为边构造等边
为边构造等边![]() ,这样就有两个等边三角形共顶点
,这样就有两个等边三角形共顶点![]() ,然后连结
,然后连结![]() ,通过转化的思想求出了
,通过转化的思想求出了![]() 的度数,则
的度数,则![]() 的度数为 度;
的度数为 度;
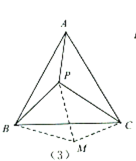
(3)深化模型:如(4),在四边形![]() 中,AD=4,CD=3,∠ABC=∠ACB=∠ADC=45°,求
中,AD=4,CD=3,∠ABC=∠ACB=∠ADC=45°,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD是经过![]() 顶点C的一条直线,且直线CD经过
顶点C的一条直线,且直线CD经过![]() 的内部,点E,F在射线CD上,已知
的内部,点E,F在射线CD上,已知![]() 且
且![]() .
.
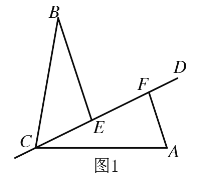
(1)如图1,若![]() ,
,![]() ,问
,问![]() ,成立吗?说明理由.
,成立吗?说明理由.
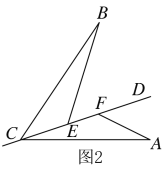
(2)将(1)中的已知条件改成![]() ,
,![]() (如图2),问
(如图2),问![]() 仍成立吗?说明理由.
仍成立吗?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场服装部为了调动营业员的积极性,决定实行目标管理,根据目标完成的情况对营业员进行适当的奖励.为了确定一个适当的月销售目标,商场服装部统计了每位营业员在某月的销售额(单位:万元),数据如下:
17 | 18 | 16 | 13 | 24 | 15 | 28 | 26 | 18 | 19 |
22 | 17 | 16 | 19 | 32 | 30 | 16 | 14 | 15 | 26 |
15 | 32 | 23 | 17 | 15 | 15 | 28 | 28 | 16 | 19 |
对这30个数据按组距3进行分组,并整理、描述和分析如下.
频数分布表
组别 | 一 | 二 | 三 | 四 | 五 | 六 | 七 |
销售额 |
|
|
|
|
|
|
|
频数 | 7 | 9 | 3 |
| 2 |
| 2 |
数据分析表
平均数 | 众数 | 中位数 |
20.3 |
| 18 |
请根据以上信息解答下列问题:
(1)填空:a= ,b= ,c= ;
(2)若将月销售额不低于25万元确定为销售目标,则有 位营业员获得奖励;
(3)若想让一半左右的营业员都能达到销售目标,你认为月销售额定为多少合适?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠A=∠D=90°,点E、F在线段BC上,DE与AF交于点O,且AB=DC,BE=CF.求证:
(1)AF=DE
(2)若OP⊥EF,求证:OP平分∠EOF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和他的同学根据抛掷两枚硬币时记录的实验结果,制作“出现两个正面”的频数、频率表如下:
抛掷次数 |
|
|
|
|
|
|
|
| |
出现两个正面的频数 |
|
|
|
|
|
|
|
| |
出现两个正面的频率 |
|
|
|
|
|
|
|
|
![]() 在大数次抛掷两枚硬币的实验中,出现两个正面的频率稳定在________附近;
在大数次抛掷两枚硬币的实验中,出现两个正面的频率稳定在________附近;
![]() 小明和表弟玩一个抛掷两枚硬币的游戏,小明制定的游戏规则如下:抛出两个正面–小明的表弟赢
小明和表弟玩一个抛掷两枚硬币的游戏,小明制定的游戏规则如下:抛出两个正面–小明的表弟赢![]() 分;抛出其他结果–小明赢
分;抛出其他结果–小明赢![]() 分;谁先到
分;谁先到![]() 分,谁就得胜.你认为这个游戏规则公平吗?说说理由.
分,谁就得胜.你认为这个游戏规则公平吗?说说理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】第7届世界军人运动会于2019年10月18日在武汉开幕,为备战本届军运会,某运动员进行了多次打靶训练,现随机抽取该运动员部分打靶成绩进行整理分析,共分成四组:![]() (优秀)、
(优秀)、![]() (良好)、
(良好)、![]() (合格)、
(合格)、![]() (不合格),绘制了如下不完整的统计图:
(不合格),绘制了如下不完整的统计图:
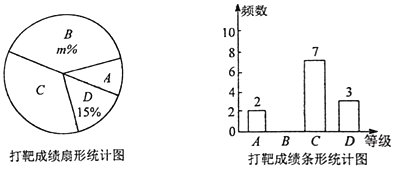
根据以上信息,解答下列问题:
(1)直接写出本次统计成绩的总次数和图中![]() 的值.
的值.
(2)求扇形统计图中![]() (合格)所对应圆心角的度数.
(合格)所对应圆心角的度数.
(3)请补全条形统计图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知△ABC中,AB=10cm,AC=8cm,BC=6cm.如果点P由B出发沿BA方向点A匀速运动,同时点Q由A出发沿AC方向向点C匀速运动,它们的速度均为2cm/s.连接PQ,设运动的时间为t(单位:s)(0≤t≤4).解答下列问题:
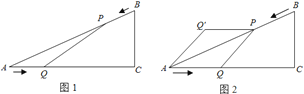
(1)当t为何值时,PQ∥BC.
(2)设△AQP面积为S(单位:cm2),当t为何值时,S取得最大值,并求出最大值.
(3)是否存在某时刻t,使线段PQ恰好把△ABC的面积平分?若存在,求出此时t的值;若不存在,请说明理由.
(4)如图2,把△AQP沿AP翻折,得到四边形AQPQ′.那么是否存在某时刻t,使四边形AQPQ′为菱形?若存在,求出此时菱形的面积;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com