
【题目】如图1,已知△ABC中,AB=10cm,AC=8cm,BC=6cm.如果点P由B出发沿BA方向点A匀速运动,同时点Q由A出发沿AC方向向点C匀速运动,它们的速度均为2cm/s.连接PQ,设运动的时间为t(单位:s)(0≤t≤4).解答下列问题:
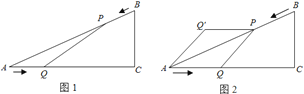
(1)当t为何值时,PQ∥BC.
(2)设△AQP面积为S(单位:cm2),当t为何值时,S取得最大值,并求出最大值.
(3)是否存在某时刻t,使线段PQ恰好把△ABC的面积平分?若存在,求出此时t的值;若不存在,请说明理由.
(4)如图2,把△AQP沿AP翻折,得到四边形AQPQ′.那么是否存在某时刻t,使四边形AQPQ′为菱形?若存在,求出此时菱形的面积;若不存在,请说明理由.
【答案】(1)![]() s(2)当t=
s(2)当t=![]() s时,S取得最大值,最大值为
s时,S取得最大值,最大值为![]() cm2(3)不存在。理由见解析(4)存在,
cm2(3)不存在。理由见解析(4)存在,![]() cm2
cm2
【解析】
解:∵AB=10cm,AC=8cm,BC=6cm,
∴由勾股定理逆定理得△ABC为直角三角形,∠C为直角。
(1)BP=2t,则AP=10﹣2t.
若PQ∥BC,则![]() ,即
,即![]() ,解得
,解得![]() 。
。
∴当![]() s时,PQ∥BC。
s时,PQ∥BC。
(2)如图1所示,过P点作PD⊥AC于点D。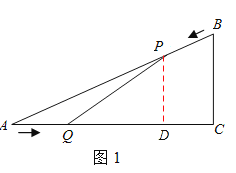
则PD∥BC,∴△APD∽△ABC。
∴![]() ,即
,即![]() ,解得
,解得![]() 。
。
∴S=![]() ×AQ×PD=
×AQ×PD=![]() ×2t×(
×2t×(![]() )
)
![]() 。
。
∴当t=![]() s时,S取得最大值,最大值为
s时,S取得最大值,最大值为![]() cm2。
cm2。
(3)不存在。理由如下:
假设存在某时刻t,使线段PQ恰好把△ABC的面积平分,
则有S△AQP=![]() S△ABC,而S△ABC=
S△ABC,而S△ABC=![]() ACBC=24,∴此时S△AQP=12。
ACBC=24,∴此时S△AQP=12。
由(2)可知,S△AQP=![]() ,∴
,∴![]() =12,化简得:t2﹣5t+10=0。
=12,化简得:t2﹣5t+10=0。
∵△=(
∴不存在某时刻t,使线段PQ恰好把△ABC的面积平分。
(4)存在。
假设存在时刻t,使四边形AQPQ′为菱形,
则有AQ=PQ=BP=2t。
如图2所示,过P点作PD⊥AC于点D,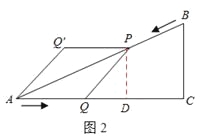
则有PD∥BC,
∴△APD∽△ABC。
∴![]() ,即
,即![]() 。
。
解得:PD=![]() ,AD=
,AD=![]() ,
,
∴QD=AD﹣AQ=![]() 。
。
在Rt△PQD中,由勾股定理得:QD2+PD2=PQ2,即(![]() )2+(
)2+(![]() )2=(2t)2,
)2=(2t)2,
化简得:13t2﹣90t+125=0,解得:t1=5,t2=![]() 。
。
∵t=5s时,AQ=10cm>AC,不符合题意,舍去,∴t=![]() 。
。
由(2)可知,S△AQP=![]()
∴S菱形AQPQ′=2S△AQP=2×(![]() )=2×[﹣
)=2×[﹣![]() ×(
×(![]() )2+6×
)2+6×![]() ]=
]=![]() 。
。
∴存在时刻t=![]() ,使四边形AQPQ′为菱形,此时菱形的面积为
,使四边形AQPQ′为菱形,此时菱形的面积为![]() cm2。
cm2。
(1)由PQ∥BC时的比例线段关系,列一元一次方程求解。
(2)如图1所示,过P点作PD⊥AC于点D,得△APD∽△ABC,由比例线段,求得PD,从而可以得到S的表达式,然后利用二次函数的极值求得S的最大值。
(3)利用(2)中求得的△AQP的面积表达式,再由线段PQ恰好把△ABC的面积平分,列出一元二次方程;由于此一元二次方程的判别式小于0,则可以得出结论:不存在这样的某时刻t,使线段PQ恰好把△ABC的面积平分。
(4)根据菱形的性质及相似三角形比例线段关系,求得PQ、QD和PD的长度;然后在Rt△PQD中,求得时间t的值;最后求菱形的面积,值得注意的是菱形的面积等于△AQP面积的2倍,从而可以利用(2)中△AQP面积的表达式,这样可以化简计算。


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
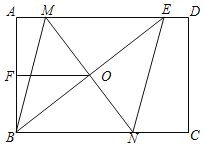
【题目】如图,在矩形ABCD中,E是AD上一点,MN垂直平分BE,分别交AD,BE,BC于点M,O,N,连接BM,EN
(1)求证:四边形BMEN是菱形.
(2)若AE=8,F为AB的中点,BF+OB=8,求MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,D,E 分别是 AB,BC 上的点,且 DE∥AC,若 S△BDE:S△CDE=1:3,则S△DEB: S△ADC=( )

A. 1:5 B. 1:9 C. 1:10 D. 1:12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2﹣6x+9与直线y=x+3交于A,B两点(点A在点B的左侧),抛物线的顶点为C,直线y=x+3与x轴交于点D.
(Ⅰ)求抛物线的顶点C的坐标及A,B两点的坐标;
(Ⅱ)将抛物线y=x2﹣6x+9向上平移1个单位长度,再向左平移t(t>0)个单位长度得到新抛物线,若新抛物线的顶点E在△DAC内,求t的取值范围;
(Ⅲ)点P(m,n)(﹣3<m<1)是抛物线y=x2﹣6x+9上一点,当△PAB的面积是△ABC面积的2倍时,求m,n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了传承中华优秀传统文化,市教育局决定开展“经典诵读进校园”活动,某校团委组织八年级100名学生进行“经典诵读”选拔赛,赛后对全体参赛学生的成绩进行整理,得到下列不完整的统计图表。
组别 | 分数段 | 频次 | 频率 |
A | 60x<70 | 17 | 0.17 |
B | 70x<80 | 30 | a |
C | 80x<90 | b | 0.45 |
D | 90x<100 | 8 | 0.08 |
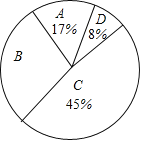
请根据所给信息,解答以下问题:
(1)表中a=___,b=___;
(2)请计算扇形统计图中B组对应扇形的圆心角的度数;
(3)已知有四名同学均取得98分的最好成绩,其中包括来自同一班级的甲、乙两名同学,学校将从这四名同学中随机选出两名参加市级比赛,请用列表法或画树状图法求甲、乙两名同学都被选中的概率。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从甲、乙、丙三个厂家生产的同一种产品中,各抽出![]() 件产品,对其使用寿命进行跟踪调查,结果如下(单位:年)
件产品,对其使用寿命进行跟踪调查,结果如下(单位:年)
甲:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
乙:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
丙:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
三家广告中都称该种产品的使用寿命是![]() 年,请根据调查结果判断三个厂家在广告中分别运用了平均数,众数和中位数的哪一种数据作代表.
年,请根据调查结果判断三个厂家在广告中分别运用了平均数,众数和中位数的哪一种数据作代表.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某高中学校为使高一新生入校后及时穿上合身的校服,现提前对某校九年级三班学生即将所穿校服型号情况进行了摸底调查,并根据调查结果绘制了如下两个不完整的统计图(校服型号以身高作为标准,共分为6种型号).
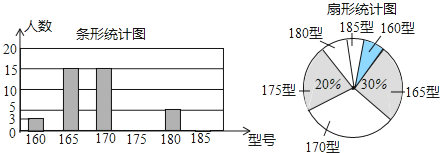
根据以上信息,解答下列问题:
(Ⅰ)该班共有 名学生,其中穿175型校服的学生有 名;
(Ⅱ)在条形统计图中,请把空缺部分补充完整.
(Ⅲ)在扇形统计图中,185型校服所对应的扇形圆心角的大小为 ;
(Ⅳ)该班学生所穿校服型号的众数为 ,中位数为 .
(Ⅴ)如果该校预计招收新生600名,根据样本数据,估计新生中穿170型校服的学生大约有 名.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的面积为8cm2 , AP垂直∠B的平分线BP于P,则△PBC的面积为( )
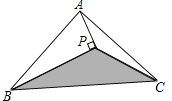
A. 2cm2 B. 3cm2 C. 4cm2 D. 5cm2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com