
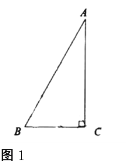
【题目】(1)在![]() 中,
中,![]() ,
,![]() (如图1),
(如图1),![]() 与
与![]() 有怎样的数量关系?试证明你的结论.
有怎样的数量关系?试证明你的结论.
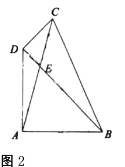
(2)图2,在四边形![]() 中,
中,![]() 相于点
相于点![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,求
,求![]() 长.
长.
【答案】(1)AB=2BC,证明见解析;(2)![]() -1.
-1.
【解析】
(1)取AB的中点D,连接DC,得AD=BD=CD,再证明△DBC是等边三角形得BD=BC,从而可证明AB=2BC;
(2)过点A作AF⊥BD于点F,先确定∠2及∠3的度数,在Rt△AFB中求出AF,BF;Rt△AEF中,求出EF,AE,在Rt△ABD中求出DB,继而得出DE.
(1)AB=2BC
证明:取AB的中点D,连接DC,
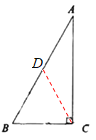
∵∠ACB=90°,CD为斜边AB上的中线
∴AD=BD=CD
∴∠A=∠ACD=30°,∠B=∠BCD
∴∠ADC=180°-∠A-∠ACD=120°
∴∠B=∠BCD=![]() ∠ADC=60°
∠ADC=60°
∴△DBC是等边三角形
∴BD=BC
∴AB=2BD=2BC
即AB=2BC
(2)过点A作AF⊥BD于点F,
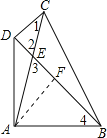
∵∠CDB=90°,∠1=30°,
∴∠2=∠3=60°,
在△AFB中,∠AFB=90°,
∵∠4=45°,AB=![]() ,
,
∴AF=BF=![]() ,
,
在Rt△AEF中,∠AFE=90°,
∴EF=1,AE=2,
在△ABD中,∠DAB=90°,AB=![]() ,
,
∴DB=2![]() ,
,
∴DE=DB-BF-EF=![]() -1.
-1.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:初中数学 来源: 题型:
【题目】课本中有一道作业题:有一块三角形余料ABC,它的边BC=120mm,高AD=80mm.要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.
(1)加工成的正方形零件的边长是多少mm?
(2)如果原题中要加工的零件是一个矩形,且此矩形是由两个并排放置的正方形所组成,如图1,此时,这个矩形零件的两条边长又分别为多少?请你计算.
(3)如果原题中所要加工的零件只是一个矩形,如图2,这样,此矩形零件的两条边长就不能确定,但这个矩形面积有最大值,求达到这个最大值时矩形零件的两条边长.
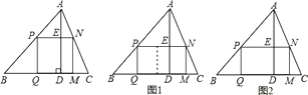
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末,小华和小亮想用所学的数学知识测量家门前小河的宽.测量时,他们选择了河对岸边的一棵大树,将其底部作为点A,在他们所在的岸边选择了点B,使得AB与河岸垂直,并在B点竖起标杆BC,再在AB的延长线上选择点D竖起标杆DE,使得点E与点C、A共线.
已知:CB⊥AD,ED⊥AD,测得BC=1m,DE=1.5m,BD=8.5m.测量示意图如图所示.请根据相关测量信息,求河宽AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB// CD,Rt△EFG的顶点F,G分别落在直线AB,CD上,GE交AB于点H,∠EFG=90°,∠E=32°.
(1)∠FGE= °
(2)若GE平分∠FGD,求∠EFB的度数.
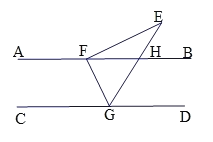
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
(1)画出△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是 ;
(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1;
(3)四边形AA2C2C的面积是 平方单位.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD的边长AB=2,E为AB的中点,F为BC的中点,AF分别与DE、BD相交于点M,N,则MN的长为( )
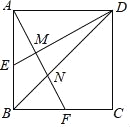
A. ![]() B.
B. ![]() ﹣1 C.
﹣1 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有3张边长为![]() 的正方形纸片(
的正方形纸片(![]() 类),5张边长为
类),5张边长为![]() 的矩形纸片(
的矩形纸片(![]() 类),5张边长为
类),5张边长为![]() 的正方形纸片(
的正方形纸片(![]() 类).
类).
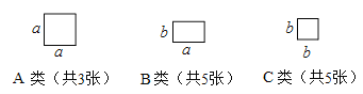
我们知道:多项式乘法的结果可以利用图形的面积表示.
例如:![]() 就能用图①或图②的面积表示.
就能用图①或图②的面积表示.
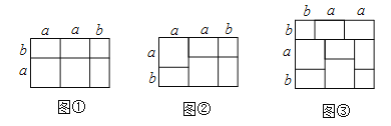
(1)请你写出图③所表示的一个等式:_______________;
(2)如果要拼一个长为![]() ,宽为
,宽为![]() 的长方形,则需要
的长方形,则需要![]() 类纸片_____张,需要
类纸片_____张,需要![]() 类纸片_____张,需要
类纸片_____张,需要![]() 类纸片_____张;
类纸片_____张;
(3)从这13张纸片中取出若干张,每类纸片至少取出一张,把取出的这些纸片拼成一个正方形(按原纸张进行无缝隙,无重叠拼接),则拼成的正方形的边长最长可以是_______(用含![]() 的式子表示).
的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义:如果两个等腰三角形的顶角相等,且项角的顶点互相重合,则称此图形为“手拉手全等模型”.因为顶点相连的四条边,形象的可以看作两双手,所以通常称为“手拉手模型”.例如,如(1),![]() 与
与![]() 都是等腰三角形,其中
都是等腰三角形,其中![]() ,则△ABD≌△ACE(SAS).
,则△ABD≌△ACE(SAS).
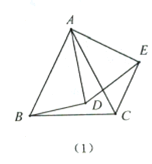
(1)熟悉模型:如(2),已知![]() 与
与![]() 都是等腰三角形,AB=AC,AD=AE,且
都是等腰三角形,AB=AC,AD=AE,且![]() ,求证:
,求证:![]() ;
;
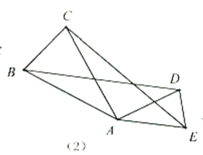
(2)运用模型:如(3),![]() 为等边
为等边![]() 内一点,且
内一点,且![]() ,求
,求![]() 的度数.小明在解决此问题时,根据前面的“手拉手全等模型”,以
的度数.小明在解决此问题时,根据前面的“手拉手全等模型”,以![]() 为边构造等边
为边构造等边![]() ,这样就有两个等边三角形共顶点
,这样就有两个等边三角形共顶点![]() ,然后连结
,然后连结![]() ,通过转化的思想求出了
,通过转化的思想求出了![]() 的度数,则
的度数,则![]() 的度数为 度;
的度数为 度;
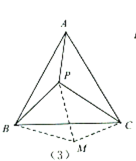
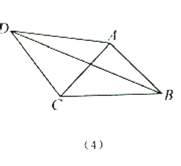
(3)深化模型:如(4),在四边形![]() 中,AD=4,CD=3,∠ABC=∠ACB=∠ADC=45°,求
中,AD=4,CD=3,∠ABC=∠ACB=∠ADC=45°,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和他的同学根据抛掷两枚硬币时记录的实验结果,制作“出现两个正面”的频数、频率表如下:
抛掷次数 |
|
|
|
|
|
|
|
| |
出现两个正面的频数 |
|
|
|
|
|
|
|
| |
出现两个正面的频率 |
|
|
|
|
|
|
|
|
![]() 在大数次抛掷两枚硬币的实验中,出现两个正面的频率稳定在________附近;
在大数次抛掷两枚硬币的实验中,出现两个正面的频率稳定在________附近;
![]() 小明和表弟玩一个抛掷两枚硬币的游戏,小明制定的游戏规则如下:抛出两个正面–小明的表弟赢
小明和表弟玩一个抛掷两枚硬币的游戏,小明制定的游戏规则如下:抛出两个正面–小明的表弟赢![]() 分;抛出其他结果–小明赢
分;抛出其他结果–小明赢![]() 分;谁先到
分;谁先到![]() 分,谁就得胜.你认为这个游戏规则公平吗?说说理由.
分,谁就得胜.你认为这个游戏规则公平吗?说说理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com