Question

【题目】如图，抛物线y=﹣x2+6x交x轴正半轴于点A，顶点为M，对称轴MB交x轴于点B．过点C（2，0）作射线CD交MB于点D（D在x轴上方），OE∥CD交MB于点E，EF∥x轴交CD于点F，作直线MF．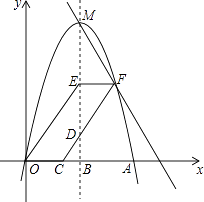

（1）求点A，M的坐标．
（2）当BD为何值时，点F恰好落在该抛物线上？
（3）当BD=1时
求直线MF的解析式，并判断点A是否落在该直线上．
（4）②延长OE交FM于点G，取CF中点P，连结PG，△FPG，四边形DEGP，四边形OCDE的面积分别记为S1 ， S2 ， S3 ， 则S1：S2：S3= ．

Answer 1

【答案】
（1）

解：令y=0，则﹣x2+6x=0，解得x=0或x=6，

∴A点坐标为（6，0），

又∵y=﹣x2+6x=﹣（x﹣3）2+9，

∴M点坐标为（3，9）

（2）

解：∵OE∥CF，OC∥EF，

∴四边形OCFE为平行四边形，且C（2，0），

∴EF=OC=2，

又B（3，0），

∴OB=3，BC=1，

∴F点的横坐标为5，

∵点F落在抛物线y=﹣x2+6x上，

∴F点的坐标为（5，5），

∴BE=5，

∵OE∥CF，

∴ ，即 = ，

∴BD= ；

（3）

解：当BD=1时，由（2）可知BE=3BD=3，

∴F（5，3），

设直线MF解析式为y=kx+b，

把M、F两点坐标代入可得 ，解得 ，

∴直线MF解析式为y=﹣3x+18，

∵当x=6时，y=﹣3×6+18=0，

∴点A落在直线MF上

（4）3：4：8
【解析】解：（4）如图所示，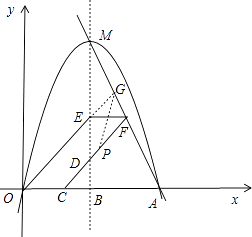

∵E（3，3），
∴直线OE解析式为y=x，
联立直线OE和直线MF解析式可得 ，解得 ，
∴G（ ， ），
∴OG= = ，OE=CF=3 ，
∴EG=OG﹣OE= ﹣3 = ，
∵ = ，
∴CD= OE= ，
∵P为CF中点，
∴PF= CF= ，
∴DP=CF﹣CD﹣PF=3 ﹣ ﹣ = ，
∵OG∥CF，
∴可设OG和CF之间的距离为h，
∴S△FPG= PFh= × h= h，
S四边形DEGP= （EG+DP）h= ×（ + ）h= h，
S四边形OCDE= （OE+CD）h= （3 + ）h=2 h，
∴S1 ， S2 ， S3= h： h：2 h=3：4：8，
所以答案是：3：4：8．