
����Ŀ����1�����ⷢ��
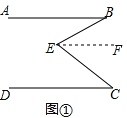
��ͼ����ֱ��AB��CD��E��AB��AD֮���һ�㣬����BE��CE�����Է�����B+��C����BEC��

��������֤�����̲���������
֤��������E��EF��AB��
��AB��DC����֪����EF��AB�������ߵ���������
��EF��DC���� ����
���C����CEF������ ����
��EF��AB�����B����BEF��ͬ������
���B+��C���� ��������������
����B+��C����BEC��
��2����չ̽��
�����E�˶���ͼ����ʾ��λ�ã������������䣬��֤����B+��C��360�㩁��BEC��
��3���������
��ͼ����AB��DC����C��120������AEC��80��������A���� ������֮��д�����ۣ�����д������̣�
���𰸡���1��ƽ����ͬһֱ�ߵ���ֱ��ƽ�У���ֱ��ƽ�У��ڴ�����ȣ���BEF+��CEF����2��֤������������3��20����
��������
��1������![]() ��
��![]() ������ƽ���ߵ��ж��ó�
������ƽ���ߵ��ж��ó�![]() ������ƽ���ߵ����ʵó����ɣ�
������ƽ���ߵ����ʵó����ɣ�
��2������![]() ��
��![]() ������ƽ���ߵ��ж��ó�
������ƽ���ߵ��ж��ó�![]() ������ƽ���ߵ����ʵó����ɣ�
������ƽ���ߵ����ʵó����ɣ�
��3������![]() ��
��![]() ������ƽ���ߵ��ж��ó�
������ƽ���ߵ��ж��ó�![]() ������ƽ���ߵ����ʵó����ɣ�
������ƽ���ߵ����ʵó����ɣ�
��1��֤������ͼ��������E��EF��AB��
��AB��DC����֪����EF��AB�������ߵ���������
��EF��DC��ƽ����ͬһֱ�ߵ���ֱ��ƽ�У���
���C����CEF������ֱ��ƽ�У��ڴ�����ȣ���
��EF��AB��
���B����BEF��ͬ������
���B+��C����BEF+��CEF������������
����B+��C����BEC��
�ʴ�Ϊ��ƽ����ͬһֱ�ߵ���ֱ��ƽ�У���ֱ��ƽ�У��ڴ�����ȣ���BEF+��CEF��
��2��֤������ͼ��������E��EF��AB��
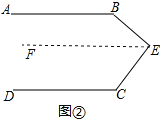
��AB��DC����֪����EF��AB�������ߵ���������
��EF��DC��ƽ����ͬһֱ�ߵ���ֱ��ƽ�У���
���C+��CEF��180������B+��BEF��180����
���B+��C+��AEC��360����
���B+��C��360�㩁��BEC��
��3���⣺��ͼ��������E��EF��AB��

��AB��DC����֪����EF��AB�������ߵ���������
��EF��DC��ƽ����ͬһֱ�ߵ���ֱ��ƽ�У���
���C+��CEF��180������A����BEF��
�ߡ�C��120������AEC��80����
���CEF��180�㩁120����60����
���BEF��80�㩁60����20����
���A����AEF��20����
�ʴ�Ϊ��20����


 �����Ծ���ĩ���100��ϵ�д�
�����Ծ���ĩ���100��ϵ�д� ˫��ͬ������ѵ��ϵ�д�
˫��ͬ������ѵ��ϵ�д� �Ƹ�С״Ԫͬ������������ϵ�д�
�Ƹ�С״Ԫͬ������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1���ھ���ֽƬABCD�У�AB=3cm��AD=5cm���۵�ֽƬʹB�����ڱ�AD�ϵ�E�����ۺ�ΪPQ������E��EF��AB��PQ��F������BF��
��1����֤���ı���BFEPΪ���Σ�
��2������E��AD�����ƶ�ʱ���ۺ۵Ķ˵�P��QҲ��֮�ƶ���
�ٵ���Q���C�غ�ʱ����ͼ2����������BFEP�ı߳���
������P��Q�ֱ��ڱ�BA��BC���ƶ��������E�ڱ�AD���ƶ��������룮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �ı�
�ı�![]() ��
��![]() Ϊ�ߵĵȱ�����
Ϊ�ߵĵȱ�����![]() �͵ȱ�������
�͵ȱ�������![]() ���ı���
���ı���![]() ��ƽ���ı��Σ�
��ƽ���ı��Σ�
![]() ��
��![]() ����ʲô����ʱ���ı���
����ʲô����ʱ���ı���![]() �Ǿ��Σ�
�Ǿ��Σ�
![]() ��
��![]() ����ʲô����ʱ��ƽ���ı���
����ʲô����ʱ��ƽ���ı���![]() �����ڣ�
�����ڣ�
![]() ��
��![]() �ֱ�����ʲô����ʱ��ƽ���ı���
�ֱ�����ʲô����ʱ��ƽ���ı���![]() �����Σ������Σ�
������������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ���ڳ�����ABCD�У�AB=4��AD=6���ӳ�BC����E��ʹCE=2������DE������P�ӵ�B��������ÿ��2����λ���ٶ���BC��CD��DA���յ�A�˶������P���˶�ʱ��Ϊt�룬��t��ֵΪ_____��ʱ����ABP����DCEȫ�ȣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�ı���ABCD�Ķ���ΪA��1��2����B����1��2����C������1����2����D��1����2������M�͵�Nͬʱ��E����������ı��εı������������˶���M����1��λ/s���ٶ�����ʱ���˶���N����2��λ/s���ٶ���˳ʱ���˶������M�͵�N��2017������ʱ������Ϊ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��֤��������ƽ���߱�������ֱ�����أ�һ��ͬλ�ǵ�ƽ������ƽ�У�

��֪����ͼ��_______________________��
��֤��_____________________________��
֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AD��BC��D��BD=AD��DG=DC��E��F�ֱ���BG��AC���е㣮
��1����֤��DE=DF��DE��DF��
��2������EF����AC=10����EF�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��BD��CE�ֱ�����ABC�ı�AC��AB�ϵĸߣ�P��BD���ӳ����ϣ���BP=AC����Q��CE�ϣ�CQ=AB,
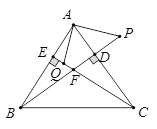
��֤����1��AP=AQ ��
��2��AP��AQ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() �Ķ��η���
�Ķ��η���![]() .
.
��1����![]() ���Ҵ˷�����һ����Ϊ
���Ҵ˷�����һ����Ϊ![]() ����
����![]() ��ֵ��
��ֵ��
��2����![]() ���жϴ˷��̸������.
���жϴ˷��̸������.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com