
【题目】如图,等边△ABC内接于⊙O,P是弧AB上任一点(点P不与点A、B重合),连接AP、BP,过点C作CM∥BP交PA的延长线于点M.
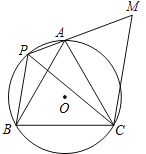
(1)求∠APC的度数.
(2)求证:△PCM为等边三角形.
(3)若PA=1,PB=3,求△PCM的面积.
【答案】(1)∠APC=60°;(2)见解析;(3)S△PCM=4![]() .
.
【解析】
(1)利用同弧所对的圆周角相等即可求得题目中的未知角;
(2)利用同弧所对的圆周角相等即可求得题目中的未知角,进而判定△PCM为等边三角形;
(2)利用上题中得到的相等的角和等边三角形中相等的线段证得两三角形全等,进而利用△PCM为等边三角形,进而求得PH的长,利用三角形的面积公式计算即可.
(1)∵△ABC是等边三角形,
∴∠ABC=60°,
∴∠APC=∠ABC=60°;
(2)∵∠BPC=∠BAC=60°,
∵CM∥BP,
∴∠PCM=∠BPC=60°,
又由(1)得∠APC=60°,
∴△PCM为等边三角形;
(3)解:∵△ABC是等边三角形,△PCM为等边三角形,
∴∠PCA+∠ACM=∠BCP+∠PCA,
∴∠BCP=∠ACM,
在△BCP和△ACM中,
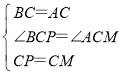 ,
,
∴△BCP≌△ACM(SAS),
∴CM=CP,AM=BP=3,
∴CM=PM=1+3=4,
作PH⊥CM于H,
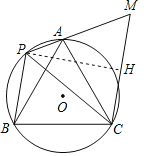
在Rt△PMH中,∠PMH=60°,PM=4,
∴PH=2![]() ,
,
∴S△PCM=![]() PHCM=
PHCM=![]() ×4×2
×4×2![]() =4
=4![]() .
.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线l:
中,直线l:![]() 与直线
与直线![]() ,直线
,直线![]() 分别交于点A,B,直线
分别交于点A,B,直线![]() 与直线
与直线![]() 交于点
交于点![]() .
.
(1)求直线![]() 与
与![]() 轴的交点坐标;
轴的交点坐标;
(2)横、纵坐标都是整数的点叫做整点.记线段![]() 围成的区域(不含边界)为
围成的区域(不含边界)为![]() .
.
①当![]() 时,结合函数图象,求区域
时,结合函数图象,求区域![]() 内的整点个数;
内的整点个数;
②若区域![]() 内没有整点,直接写出
内没有整点,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+2ax+c的图象与x轴交于A、B两点(点A在点B的左边)AB=4,与y轴交于点C,OC=OA,点D为抛物线的顶点.
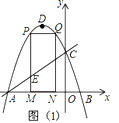
(1)求抛物线的解析式;
(2)点M(m,0)为线段AB上一点(点M不与点A、B重合),过点M作x轴的垂线,与直线AC交于点E,与抛物线交于点P,过点P作PQ∥AB交抛物线于点Q,过点Q作QN⊥x轴于点N,可得矩形PQNM,如图1,点P在点Q左边,当矩形PQNM的周长最大时,求m的值,并求出此时的△AEM的面积;
(3)在(2)的条件下,当矩形PMNQ的周长最大时,连接DQ,过抛物线上一点F作y轴的平行线,与直线AC交于点G(点G在点F的上方),若FG=![]() DQ,求点F的坐标.
DQ,求点F的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC是⊙O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD=16cm,AE=4cm.
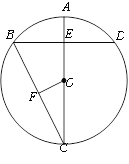
(1)求⊙O的半径;
(2)求OF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,且
点,且![]() .
.
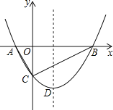
(1)求抛物线的解析式和顶点![]() 的坐标;
的坐标;
(2)判断![]() 的形状,证明你的结论;
的形状,证明你的结论;
(3)点![]() 是
是![]() 轴上的一个动点,当
轴上的一个动点,当![]() 的周长最小时,求
的周长最小时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
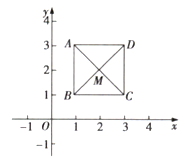
【题目】如图,已知正方形ABCD的顶点![]() ,
,![]() ,
,![]() ,规定“把正方形ABCD先沿x轴翻折,再向左平移1个单位长度”为一次变换,如此这样,连续经过2019次变换后,正方形ABCD的对角线的交点M的坐标为( )
,规定“把正方形ABCD先沿x轴翻折,再向左平移1个单位长度”为一次变换,如此这样,连续经过2019次变换后,正方形ABCD的对角线的交点M的坐标为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“互联网+”时代,网上购物备受消费者青睐.某网店专售一款休闲裤,其成本为每条40元,当售价为每条80元时,每月可销售100条.为了吸引更多顾客,该网店采取降价措施.据市场调查反映:销售单价每降1元,则每月可多销售5条.设每条裤子的售价为![]() 元(
元(![]() 为正整数),每月的销售量为
为正整数),每月的销售量为![]() 条.
条.
(1)直接写出![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)设该网店每月获得的利润为![]() 元,当销售单价降低多少元时,每月获得的利润最大,最大利润是多少?
元,当销售单价降低多少元时,每月获得的利润最大,最大利润是多少?
(3)该网店店主热心公益事业,决定每月从利润中捐出200元资助贫困学生.为了保证捐款后每月利润不低于4220元,且让消费者得到最大的实惠,该如何确定休闲裤的销售单价?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com