
【题目】如图,AC是⊙O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD=16cm,AE=4cm.
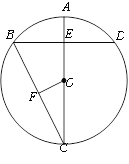
(1)求⊙O的半径;
(2)求OF的长.
 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边CD与Rt△EFG的直角边EF重合,将正方形ABCD以1cm/s的速度沿FE方向移动,在移动过程中,边CD始终与边EF重合(移动开始时点C与点F重合).连接AE,过点C作AE的平行线交直线EG于点H,连接HD.已知正方形ABCD的边长为1cm,EF=4cm,设正方形移动时间为x(s),线段EH的长为y(cm),其中0≤x≤2.5.
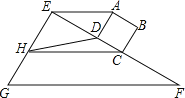
(1)当x=2时,AE的长为 ;
(2)试求出y关于x的函数关系式,并求出△EHD与△ADE的面积之差;
(3)当正方形ABCD移动时间x= 时,线段HD所在直线经过点B.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】山西特产专卖店销售核桃,其进价为每千克40元,按每千克60元出售,平均每天可售出100千克,后来经过市场调查发现,单价每降低2元,则平均每天的销售可增加20千克,若该专卖店销售这种核桃要想平均每天获利2240元,请回答:
(1)每千克核桃应降价多少元?
(2)在平均每天获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的几折出售?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的对角线AC和BD相交于点O,O又是正方形A1B1C1O的一个顶点,OA1交AB于点E,OC1交BC于点F.
(1)求证:△AOE≌△BOF;
(2)如果两个正方形的边长都为a,那么正方形A1B1C1O绕O点转动,两个正方形重叠部分的面积等于多少?
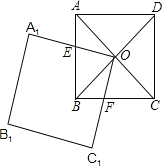
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠B=∠C=30°,点O是BC边上一点,以点O为圆心、OB为半径的圆经过点A,与BC交于点D.
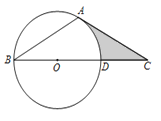
⑴ 试说明AC与⊙O相切;
⑵ 若![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC内接于⊙O,P是弧AB上任一点(点P不与点A、B重合),连接AP、BP,过点C作CM∥BP交PA的延长线于点M.
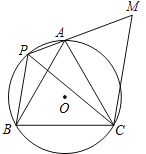
(1)求∠APC的度数.
(2)求证:△PCM为等边三角形.
(3)若PA=1,PB=3,求△PCM的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,H是对角线BD的中点,延长DC至E,使得DE=DB,连接BE,作DF⊥BE交BC于点G,交BE于点F,连接CH、FH,下列结论:(1)HC=HF;(2)DG=2EF;(3)BE·DF=2CD2;(4)S△BDE=4S△DFH;(5)HF∥DE,正确的个数是( )

A.5B.4C.3D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】盒中有若干枚黑棋和白棋,这些棋除颜色外无其他差别,现让学生进行摸棋试验:每次摸出一枚棋,记录颜色后放回摇匀.重复进行这样的试验得到以下数据:
摸棋的次数n | 100 | 200 | 300 | 500 | 800 | 1000 |
摸到黑棋的次数m | 24 | 51 | 76 | 124 | 201 | 250 |
摸到黑棋的频率 | 0.240 | 0.255 | 0.253 | 0.248 | 0.251 | 0.250 |
(1)根据表中数据估计从盒中摸出一枚棋是黑棋的概率是 ;(精确到0.01)
(2)若盒中黑棋与白棋共有4枚,某同学一次摸出两枚棋,请计算这两枚棋颜色不同的概率,并说明理由
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com