
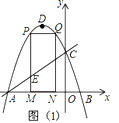
����Ŀ����ͼ��������y��ax2+2ax+c��ͼ����x�ύ��A��B���㣨��A�ڵ�B����ߣ�AB��4����y�ύ�ڵ�C��OC��OA����DΪ�����ߵĶ��㣮
��1���������ߵĽ���ʽ��
��2����M��m��0��Ϊ�߶�AB��һ�㣨��M�����A��B�غϣ�������M��x��Ĵ��ߣ���ֱ��AC���ڵ�E���������߽��ڵ�P������P��PQ��AB���������ڵ�Q������Q��QN��x���ڵ�N���ɵþ���PQNM����ͼ1����P�ڵ�Q��ߣ�������PQNM���ܳ����ʱ����m��ֵ���������ʱ����AEM�������
��3����(2)��������,������PMNQ���ܳ����ʱ,����DQ,����������һ��F��y���ƽ����,��ֱ��AC���ڵ�G(��G�ڵ�F���Ϸ�),��FG=![]() DQ,���F������.
DQ,���F������.
���𰸡���1��y=-x2-2x+3����2��m=-2����AEM�����Ϊ![]() ����3��F��-4��-5����1��0����
����3��F��-4��-5����1��0����
��������
��1������������y=ax2+2ax+c���ɵ�C��0��c�����Գ���Ϊx=-1���ٸ���OC=OA��AB=4���ɵ�A��-3��0����������������y=ax2+2ax+3���������ߵĽ���ʽΪy=-x2-2x+3��
��2�����ݵ�M��m��0�����ɵþ���PQNM�У�P��m��-m2-2m+3����Q��-2-m��-m2-2m+3�����ٸ��ݾ���PQNM���ܳ�=2��PM+PQ��=-2��m+2��2+10���ɵõ�m=-2ʱ������PQNM���ܳ������ֵ10��M������Ϊ��-2��0���������ֱ��ACΪy=x+3��AM=1�����E��-2��1����ME=1���ݴ������AEM�������
��3���ڣ�2���Ļ����ϣ��жϳ�NӦ��ԭ���غϣ�Q����C���غϣ����DQ=DC=![]() ���ٽ������̣�n+3��-��-n2-2n+3��=4���ɣ�
���ٽ������̣�n+3��-��-n2-2n+3��=4���ɣ�
�⣺��1����������y=ax2+2ax+c���ɵ�C��0��c�����Գ���Ϊx=![]() =-1��
=-1��
��OC=OA��
��A��-c��0����B��-2+c��0����
��AB=4��
��-2+c-��-c��=4��
��c=3��
��A��-3��0����
����������y=ax2+2ax+3����
0=9a-6a+3��
���a=-1��
�������ߵĽ���ʽΪy=-x2-2x+3��
��2����ͼ1����M��m��0����PM��x�ᣬ

��P��m��-m2-2m+3����
�֡߶Գ���Ϊx=-1��PQ��AB��
��Q��-2-m��-m2-2m+3����
�֡�QN��x�ᣬ
�����PQNM���ܳ�
=2��PM+PQ��
=2[��-m2-2m+3��+��-2-m-m��]
=2��-m2-4m+1��
=-2��m+2��2+10��
�൱m=-2ʱ������PQNM���ܳ������ֵ10��
��ʱ��M��-2��0����
��A��-3��0����C��0��3�����ɵ�
ֱ��ACΪy=x+3��AM=1��
�൱x=-2ʱ��y=1����E��-2��1����ME=1��
���AEM�����= ![]() ��
��
��3����M��-2��0���������ߵĶԳ���Ϊx=-l��
��NӦ��ԭ���غϣ�Q����C���غϣ�
��DQ=DC��
��x=-1����y=-x2-2x+3�����y=4��
��D��-1��4����
��DQ=DC=![]() ��
��
��FG=2![]() DQ��
DQ��
��FG=4��
��F��n��-n2-2n+3������G��n��n+3����
�ߵ�G�ڵ�F���Ϸ���FG=4��
�ࣨn+3��-��-n2-2n+3��=4��
���n=-4��n=1��
��F��-4��-5����1��0����


 �����̸�Ӯ����ٸ�Ч�����ܸ�ϰ���ϿƼ�������ϵ�д�
�����̸�Ӯ����ٸ�Ч�����ܸ�ϰ���ϿƼ�������ϵ�д� �����ҵ�����������ѧ���ӳ�����ϵ�д�
�����ҵ�����������ѧ���ӳ�����ϵ�д� ����ѧ��Ӯ�����ϵ�д�
����ѧ��Ӯ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ij��Ϊ������ȫ�������������ƺţ���ĩ����ί��֯־Ը�߽��������.����������ʦ������4��Ů��ɲ���С�á�С�ݡ�С��Сٻ����ͨ����ǩ�ķ�ʽȷ��2��Ů��ȥ�μ�.
��ǩ����4��Ů��ɲ������ֱ�д��4����ȫ��ͬ�Ŀ�Ƭ���棬�����ſ�Ƭ���泯�ϣ�ϴ�Ⱥ���������ϣ�����ʦ�ȴ��������ȡһ�ſ�Ƭ�������������ٴ�ʣ���3�ſ�Ƭ�������ȡ�ڶ��ţ���������.
��1���ð�������С�ձ��������� �¼�����С�ñ��������� �¼�(������������������Ȼ�����������)����һ�γ�ȡ��Ƭ��С�ñ��������ĸ���Ϊ ��
��2�����û���״ͼ���б��ķ�����ʾ��γ�ǩ���п��ܵĽ�����������С�ݱ��������ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾�����һ���Ʒ��ÿ���ɱ���50Ԫ���������ڼ䣬���г����飬���۵�����60Ԫʱ��ÿ���������250���������۵���ÿ����1Ԫ��ÿ������۳�5������˾�������۵���x��Ԫ��������60Ԫ�����г�Ҫ��x���ó���100Ԫ��
��1�����ÿ���������y�����������۵���x��Ԫ��֮��ĺ�����ϵʽ����д��x��ȡֵ��Χ��
��2�����ÿ�����������W��Ԫ�������۵���x��Ԫ��֮��ĺ�����ϵʽ���������xΪ����ʱ��ÿ��������������������ֵ��
��3�����ù�˾Ҫ��ÿ�������������4000Ԫ����ÿ����ܳɱ�������6250Ԫ�������۵���x��Ϳɶ�Ϊ����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ɽ���ز�ר�������ۺ��ң������Ϊÿǧ��40Ԫ����ÿǧ��60Ԫ���ۣ�ƽ��ÿ����۳�100ǧ�ˣ����������г����鷢�֣�����ÿ����2Ԫ����ƽ��ÿ������ۿ�����20ǧ�ˣ�����ר�����������ֺ���Ҫ��ƽ��ÿ�����2240Ԫ����ش�
��1��ÿǧ�˺���Ӧ���۶���Ԫ��
��2����ƽ��ÿ��������������£�Ϊ�����������ڹ˿ͣ�Ӯ���г����õ�Ӧ��ԭ�ۼ۵ļ��۳��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
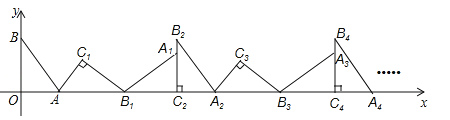
����Ŀ�� ��ͼ����ƽ��ֱ������ϵ�У�����ABO�Ƶ�A˳ʱ����ת����AB1C1��λ�ã���B��O�ֱ����ڵ�B1��C1������B1��x���ϣ��ٽ���AB1C1�Ƶ�B1˳ʱ����ת����A1B1C2��λ�ã���C2��x���ϣ�����A1B1C2�Ƶ�C2˳ʱ����ת����A2B2C2��λ�ã���A2��x���ϣ����ν�����ȥ��������A��![]() ��0����B��0��2�������B2016������Ϊ____________________��
��0����B��0��2�������B2016������Ϊ____________________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
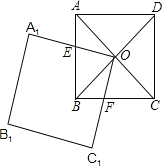
����Ŀ����ͼ��������ABCD�ĶԽ���AC��BD�ཻ�ڵ�O��O����������A1B1C1O��һ�����㣬OA1��AB�ڵ�E��OC1��BC�ڵ�F��
(1)��֤����AOE�ա�BOF��
(2)������������εı߳���Ϊa����ô������A1B1C1O��O��ת���������������ص����ֵ�������ڶ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У���B����C��30������O��BC����һ�㣬�Ե�OΪԲ�ġ�OBΪ�뾶��Բ������A����BC���ڵ�D.
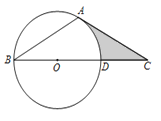
�� ��˵��AC���O���У�
�� ��![]() ����ͼ����Ӱ���ֵ����.
����ͼ����Ӱ���ֵ����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ȱ���ABC�ڽ��ڡ�O��P�ǻ�AB����һ�㣨��P�����A��B�غϣ�������AP��BP������C��CM��BP��PA���ӳ����ڵ�M��
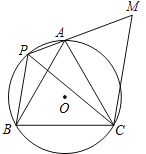
��1�����APC�Ķ�����
��2����֤����PCMΪ�ȱ������Σ�
��3����PA��1��PB��3������PCM�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
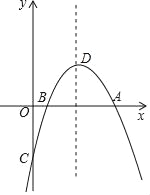
����Ŀ����ͼ��������y=ax2+bx+c��x�ύ��A��B��1��0�����㣬��y�ύ�ڵ�C��ֱ��y=![]() x��2����A��C���㣬�����ߵĶ���ΪD��
x��2����A��C���㣬�����ߵĶ���ΪD��
��1���������ߵĽ���ʽ��
��2���������ߵĶ���D�����ꣻ
��3����y�����Ƿ����һ��G��ʹ��GD+GB��ֵ��С�������ڣ������G�����ꣻ�������ڣ���˵�����ɣ�
��4����ֱ��AC���Ϸ����������Ƿ���ڵ�P��ʹ��PAC�������������ڣ�ֱ��д��P�����꼰��PAC��������ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com