
����Ŀ��ij��˾�����һ���Ʒ��ÿ���ɱ���50Ԫ���������ڼ䣬���г����飬���۵�����60Ԫʱ��ÿ���������250���������۵���ÿ����1Ԫ��ÿ������۳�5������˾�������۵���x��Ԫ��������60Ԫ�����г�Ҫ��x���ó���100Ԫ��
��1�����ÿ���������y�����������۵���x��Ԫ��֮��ĺ�����ϵʽ����д��x��ȡֵ��Χ��
��2�����ÿ�����������W��Ԫ�������۵���x��Ԫ��֮��ĺ�����ϵʽ���������xΪ����ʱ��ÿ��������������������ֵ��
��3�����ù�˾Ҫ��ÿ�������������4000Ԫ����ÿ����ܳɱ�������6250Ԫ�������۵���x��Ϳɶ�Ϊ����Ԫ��
���𰸡���1��y����5x+550����60��x��100������2����x��80ʱ��y�����ֵΪ4500Ԫ����3������x��Ϳɶ�Ϊ85Ԫ��
��������
��1���ɡ�ÿ����1Ԫ����������5������֪������ΪxԪʱ����5��x��60�����������ӵļ�������ԭ�������ɱ�ʾ��������y��
��2�����ݡ�ÿ������=���ۼ۩��ɱ��������������г���������ʽ���ٶԶ��κ��������䷽���������������ֵ��
��3����W=4000�����x��ֵ���ٸ���������ͼ��д��W��4000ʱx��ȡֵ��Χ���ٸ����ܳɱ�������6250�г�����ʽ��������������ʽ�������x��ȡֵ��Χ���Ӷ�ȷ��x����Сֵ��
��1��y=250��5��x��60������y=��5x+550��60��x��100����
��2��W=��x��50������5x+550������y=��5x2+800x��27500��
�䷽�ã�W=��5��x��80��2+4500��
��a=��5���������߿������£��൱x=80ʱ��y�����ֵΪ4500Ԫ��
��3����W=4000ʱ����5��x��80��2+4500=4000����ã�x1=70��x2=90��
��������ͼ���֪����W��4000Ԫʱ��x��ȡֵ��ΧΪ70��x��90��
�֡�50����5x+550����6250����ã�x��85����xȡֵ��ΧΪ85��x��90�����x��Ϳɶ�Ϊ85Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y��ax2+bx+4 ������A����3��0������ B ���������ϣ�CB��x�ᣬ��AB ƽ����CAO����������ߵĽ���ʽ��___________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ɱ߳�Ϊ1����λ���ȵ�С��������ɵ������У������˸����ABC�������������ߵĽ��㣩�͵�A1��
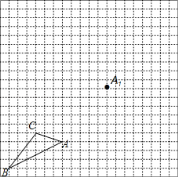
��1������ABC�Ƶ�A˳ʱ����ת90����������Ӧ����AB1C1��
��2������AB1C1������AA1ƽ�Ƶ���A1B2C2����������A1B2C2��
��3����C�����α任��������������·����Ϊ�� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ![]() �У�ֱ��l��
�У�ֱ��l��![]() ��ֱ��
��ֱ��![]() ��ֱ��
��ֱ��![]() �ֱ��ڵ�A��B��ֱ��
�ֱ��ڵ�A��B��ֱ��![]() ��ֱ��
��ֱ��![]() ���ڵ�
���ڵ�![]() ��
��
��1����ֱ��![]() ��
��![]() ��Ľ������ꣻ
��Ľ������ꣻ
��2���ᡢ�����궼�������ĵ�������㣮���߶�![]() Χ�ɵ��������߽磩Ϊ
Χ�ɵ��������߽磩Ϊ![]() ��
��
����![]() ʱ����Ϻ���ͼ��������
ʱ����Ϻ���ͼ��������![]() �ڵ����������
�ڵ����������
��������![]() ��û�����㣬ֱ��д��
��û�����㣬ֱ��д��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=x2-4x-3������˵������ȷ���ǣ� ��
A.�ú���ͼ��Ŀ�������B.�ú���ͼ��Ķ���������(-2��-7)
C.��x<0ʱ��y��x�����������D.�ú���ͼ����x����������ͬ�Ľ��㣬�ҷֲ�������ԭ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
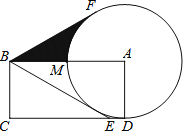
����Ŀ����ͼ���ھ���ABCD�У�E��CD���ϵĵ㣬��BE=BA=2BC=4���Ե�AΪԲ�ġ�AD��Ϊ�뾶�� ��A��AB�ڵ�M������B����A������BF���е�ΪF��
��1����˵��ֱ��BE�ǡ�A�����ߡ�
��2����ͼ����Ӱ���ֵ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�Ƕ��κ���y����x+m��2+k��ͼ���䶥������ΪM��1����4����
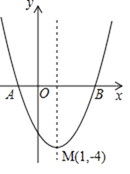
��1�����ͼ����x��Ľ���A��B�����ꣻ
��2����y���ϴ���һ��Q��ʹ�á�QMB�ܳ���С�����Q�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y��ax2+2ax+c��ͼ����x�ύ��A��B���㣨��A�ڵ�B����ߣ�AB��4����y�ύ�ڵ�C��OC��OA����DΪ�����ߵĶ��㣮
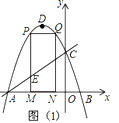
��1���������ߵĽ���ʽ��
��2����M��m��0��Ϊ�߶�AB��һ�㣨��M�����A��B�غϣ�������M��x��Ĵ��ߣ���ֱ��AC���ڵ�E���������߽��ڵ�P������P��PQ��AB���������ڵ�Q������Q��QN��x���ڵ�N���ɵþ���PQNM����ͼ1����P�ڵ�Q��ߣ�������PQNM���ܳ����ʱ����m��ֵ���������ʱ����AEM�������
��3����(2)��������,������PMNQ���ܳ����ʱ,����DQ,����������һ��F��y���ƽ����,��ֱ��AC���ڵ�G(��G�ڵ�F���Ϸ�),��FG=![]() DQ,���F������.
DQ,���F������.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com