
【题目】如图,在Rt△ABC中,∠C=90°,∠A=45°,AC=10cm,点D从点A出发沿AC方向以1cm/s的速度向点C匀速运动,同时点E从点B出发沿BA方向以![]() cm/s的速度向点A匀速运动,当其中一个点到达终点时,另一个点也随之停止运动,设点D,E运动的时间是t(0<1≤10)s.过点E作EF⊥BC于点F,连接DE,DE。
cm/s的速度向点A匀速运动,当其中一个点到达终点时,另一个点也随之停止运动,设点D,E运动的时间是t(0<1≤10)s.过点E作EF⊥BC于点F,连接DE,DE。
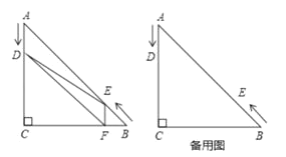
(1)用含t的式子填空:BE=________cm ,CD=________cm。
(2)试说明,无论t为何值,四边形ADEF都是平行四边形;
(3)当t为何值时,△DEF为直角三角形?请说明理由。
【答案】(1)(1)![]() t ,10-t;(2)见解析;(3)满足条件的t的值为5s或
t ,10-t;(2)见解析;(3)满足条件的t的值为5s或![]() s,理由见解析
s,理由见解析
【解析】
(1) 点D从点A出发沿AC方向以1cm/s的速度向点C匀速运动 ,由路程=时间×速度,得AD=t, CD=10-t,; 点E从点B出发沿BA方向以![]() cm/s的速度向点A匀速运动,所以BE=
cm/s的速度向点A匀速运动,所以BE=![]() t;
t;
(2)因为 △ABC 是等腰直角三角形,得∠B=45°,结合BE= ![]() t,得EF=t,又因为∠EFB和∠C都是直角相等,得 AD∥EF,根据一组对边平行且相等的四边形是平行四边形,证得四边形ADFE是平行四边形;
t,得EF=t,又因为∠EFB和∠C都是直角相等,得 AD∥EF,根据一组对边平行且相等的四边形是平行四边形,证得四边形ADFE是平行四边形;
(3) ①当∠DEF=90°时,因为DF平分对角,四边形EFCD是正方形,这时 AD=DE=CD=5,求得t=5;②当∠EDF=90°时,由DF∥AE,两直线平行,内错角相等,得∠AED=∠EDF=90°,结合∠A=45°,AD=![]() AE , 据此列式求得t值即可; ③当∠EFD=90°,点D、E、F在一条直线上,△DFE不存在.
AE , 据此列式求得t值即可; ③当∠EFD=90°,点D、E、F在一条直线上,△DFE不存在.
(1)由题意可得BE=![]() tcm,CD=AC-AD=(10-t)cm,
tcm,CD=AC-AD=(10-t)cm,
故填:![]() t ,10-t;
t ,10-t;
(2)解:如图2中

∵CA=CB,∠C=90°
∴∠A=∠B=45°,
∵EF⊥BC,
∴∠EFB=90°
∴∠FEB=∠B=45°
∴EF=BF
∵BE=![]() t,
t,
∴EF=BF=t
∴AD=EF
∵∠EFB=∠C=90°
∴AD∥EF,
∴四边形ADFE是平行四边形
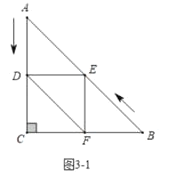
(3)解:①如图3-1中,当∠DEF=90°时,四边形EFCD是正方形,此时AD=DE=CD,
∴t=10-t,∴t=5
②如图3-2中,当∠EDF=90°时,
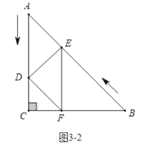
∵DF∥AC,
∴∠AED=∠EDF=90°,
∵∠A=45°
∴AD=![]() AE,
AE,
∴t=![]() (10
(10![]() -
- ![]() t),
t),
解得t= ![]()
③当∠EFD=90°,△DFE不存在
综上所述,满足条件的t的值为5s或![]() s.
s.


科目:初中数学 来源: 题型:
【题目】随着通讯技术的迅猛发展,人与人之间的沟通方式更多样、便捷.某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选一种),在全校范围内随机调查了部分学生,将统计结果绘制了如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:

(1)这次统计共抽查了 名学生;在扇形统计图中,表示“QQ”的扇形圆心角的度数为 ;
(2)将条形统计图补充完整;
(3)该校共有1500名学生,请估计该校最喜欢用“微信”进行沟通的学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在边长为1的小正方形组成的正方形网格中,建立如图所示的平面直角坐标系,已知△ABC的三个顶点都在格点上。
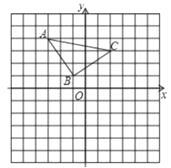
(1)请作出△ABC关于x轴对称的△A′B′C′,并分别写出点A′,B′,C′的坐标。
(2)在格点上是否存在一点D,使A,B,C,D四点为顶点的四边形是平行四边形,若存在,直接写出D点的坐标(只需写出一点即可)。
查看答案和解析>>
科目:初中数学 来源: 题型:
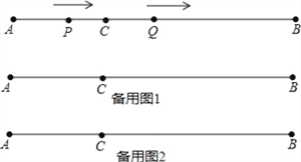
【题目】如图,AB=12cm,点C是线段AB上的一点,BC=2AC.动点P从点A出发,以3cm/s的速度向右运动,到达点B后立即返回,以3cm/s的速度向左运动;动点Q从点C出发,以1cm/s的速度向右运动.设它们同时出发,运动时间为ts.当点P与点Q第二次重合时,P、Q两点停止运动.
(1)AC=__cm,BC=__cm;
(2)当t为何值时,AP=PQ;
(3)当t为何值时,PQ=1cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:我们知道一般地,加减运算是互逆运算,乘除运算也是互逆运算;其实乘方运算也有逆运算;如我们规定式子23=8可以变形为log28=3, log525=2也可以变形为52=25.在式子23=8中, 3叫做以2为底8的对数,记为log2 8.一般地,若an=b(a>0且a≠1,b>0),则![]() 叫做以a为底b的对数,记为logab ,即 logab=n.根据上面的规定,请解决下列问题:
叫做以a为底b的对数,记为logab ,即 logab=n.根据上面的规定,请解决下列问题:
(1)计算:log3 1= , log2 32=________, log216+ log24 = ,
(2)小明在计算log1025+log104 的时候,采用了以下方法:
设log1025=x, log104=y
∴ 10x=25 10y=4
∴ 10x+y=10x×10y=25×4=100=102
∴ x+y=2
∴ log1025+log104=2通过以上计算,我们猜想logaM+ logaN=__________,请证明你的猜想.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com