练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，ABCD的对角线AC、BD相交于点O，点E是CD的中点，BC=10cm．求OE的长．

    【答案】解：∵ABCD的对角线AC、BD相交于点O， ∴OB=OD，
    ∵点E是CD的中点，
    ∴CE=DE，
    ∴OE是△BCD的中位线，
    ∵BC=10cm，
    ∴OE= BC=5cm
    【解析】先说明OE是△BCD的中位线，再根据三角形的中位线平行于第三边并且等于第三边的一半求解．
    【考点精析】关于本题考查的三角形中位线定理和平行四边形的性质，需要了解连接三角形两边中点的线段叫做三角形的中位线；三角形中位线定理：三角形的中位线平行于三角形的第三边，且等于第三边的一半；平行四边形的对边相等且平行；平行四边形的对角相等，邻角互补；平行四边形的对角线互相平分才能得出正确答案．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】有这样一道题，计算（2x4﹣4x3y﹣x2y2）﹣2（x4﹣2x3y﹣y3）+x2y2的值，其中x=2，y=﹣1，甲同学把“x=2”错抄成“x=﹣2”，但他计算的结果也是正确的，请用计算说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】猜谜语（打两个数学名词）从最后一个数起：________两牛相斗：________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在四边形ABCD中，∠A=∠C=90°，∠ABC，∠ADC的平分线分别与AD，BC相交于E，F两点，FG⊥BE于点G，∠1与∠2之间有怎样的数量关系？为什么？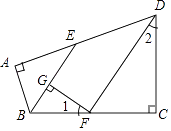

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，二次函数y=ax2+bx+c的图象经过点A（﹣1，0），B（0，﹣ ），C（2，0），其对称轴与x轴交于点D

    （1）求二次函数的表达式及其顶点坐标；

    （2）若P为y轴上的一个动点，连接PD，求PB+PD的最小值；

    （3）M（x，t）为抛物线对称轴上一动点

    ①若平面内存在点N，使得以A，B，M，N为顶点的四边形为菱形，则这样的点N共有　 　个；

    ②连接MA，MB，若∠AMB不小于60°，求t的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如果x﹣y=3，m+n=2，则（x+m）﹣（y﹣n）的值是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】水位上升30cm记作+30cm，那么﹣16cm表示 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB=BC，D、E、F分别是BC、AC、AB边上的中点．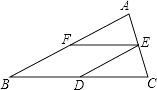
    （1）求证：四边形BDEF是菱形；
    （2）若AB=12cm，求菱形BDEF的周长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

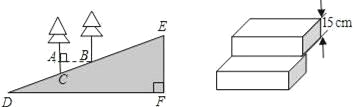
    【题目】在徒骇河观景堤坝上有一段斜坡，为了方便游客通行，现准备铺上台阶，某施工队测得斜坡上铅锤的两棵树间水平距离AB=4米，斜坡距离BC=4.25米，斜坡总长DE=85米．

    （1）求坡角∠D的度数（结果精确到1°）

    （2）若这段斜坡用厚度为15cm的长方体台阶来铺，需要铺几级台阶？（最后一个高不足15cm时，按一个台阶计算）

    （参考数据：cos20°≈0.94，sin20°≈0.34，sin18°≈0.31，cos18°≈0.95）

    查看答案和解析>>

    同步练习册答案