
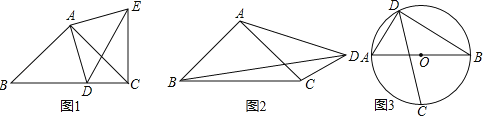
【题目】如图1:在Rt△ABC中,AB=AC,D为BC边上一点(不与点B,C重合),试探索AD,BD,CD之间满足的等量关系,并证明你的结论.小明同学的思路是这样的:将线段AD绕点A逆时针旋转90°,得到线段AE,连接EC,DE.继续推理就可以使问题得到解决.
(1)请根据小明的思路,试探索线段AD,BD,CD之间满足的等量关系,并证明你的结论;
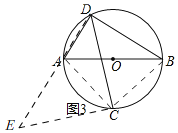
(2)如图2,在Rt△ABC中,AB=AC,D为△ABC外的一点,且∠ADC=45°,线段AD,BD,CD之间满足的等量关系又是如何的,请证明你的结论;
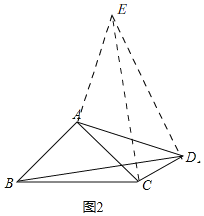
(3)如图3,已知AB是⊙O的直径,点C,D是⊙O上的点,且∠ADC=45°.
①若AD=6,BD=8,求弦CD的长为 ;
②若AD+BD=14,求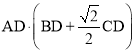 的最大值,并求出此时⊙O的半径.
的最大值,并求出此时⊙O的半径.
【答案】(1)CD2+BD2=2AD2,见解析;(2)BD2=CD2+2AD2,见解析;(3)①7![]() ,②最大值为
,②最大值为![]() ,半径为
,半径为![]()
【解析】
(1)先判断出∠BAD=CAE,进而得出△ABD≌△ACE,得出BD=CE,∠B=∠ACE,再根据勾股定理得出DE2=CD2+CE2=CD2+BD2,在Rt△ADE中,DE2=AD2+AE2=2AD2,即可得出结论;
(2)同(1)的方法得,ABD≌△ACE(SAS),得出BD=CE,再用勾股定理的出DE2=2AD2,CE2=CD2+DE2=CD2+2AD2,即可得出结论;
(3)先根据勾股定理的出DE2=CD2+CE2=2CD2,再判断出△ACE≌△BCD(SAS),得出AE=BD,
①将AD=6,BD=8代入DE2=2CD2中,即可得出结论;
②先求出CD=7![]() ,再将AD+BD=14,CD=7
,再将AD+BD=14,CD=7![]() 代入
代入![]() ,化简得出﹣(AD﹣
,化简得出﹣(AD﹣![]() )2+
)2+![]() ,进而求出AD,最后用勾股定理求出AB即可得出结论.
,进而求出AD,最后用勾股定理求出AB即可得出结论.
解:(1)CD2+BD2=2AD2,
理由:由旋转知,AD=AE,∠DAE=90°=∠BAC,
∴∠BAD=∠CAE,
∵AB=AC,
∴△ABD≌△ACE(SAS),
∴BD=CE,∠B=∠ACE,
在Rt△ABC中,AB=AC,
∴∠B=∠ACB=45°,
∴∠ACE=45°,
∴∠DCE=∠ACB+∠ACE=90°,
根据勾股定理得,DE2=CD2+CE2=CD2+BD2,
在Rt△ADE中,DE2=AD2+AE2=2AD2,
∴CD2+BD2=2AD2;
(2)BD2=CD2+2AD2,
理由:如图2,
将线段AD绕点A逆时针旋转90°,得到线段AE,连接EC,DE,
同(1)的方法得,ABD≌△ACE(SAS),
∴BD=CE,在Rt△ADE中,AD=AE,
∴∠ADE=45°,
∴DE2=2AD2,
∵∠ADC=45°,
∴∠CDE=∠ADC+∠ADE=90°,
根据勾股定理得,CE2=CD2+DE2=CD2+2AD2,
即:BD2=CD2+2AD2;
(3)如图3,过点C作CE⊥CD交DA的延长线于E,
∴∠DCE=90°,
∵∠ADC=45°,
∴∠E=90°﹣∠ADC=45°=∠ADC,
∴CD=CE,
根据勾股定理得,DE2=CD2+CE2=2CD2,
连接AC,BC,
∵AB是⊙O的直径,
∴∠ACB=∠ADB=90°,
∵∠ADC=45°,
∴∠BDC=45°=∠ADC,
∴AC=BC,
∵∠DCE=∠ACB=90°,
∴∠ACE=∠BCD,
∴△ACE≌△BCD(SAS),
∴AE=BD,
①AD=6,BD=8,
∴DE=AD+AE=AD+BD=14,
∴2CD2=142,
∴CD=7![]() ,
,
故答案为7![]() ;
;
②∵AD+BD=14,
∴CD=7![]() ,
,
∴![]() =AD(BD+
=AD(BD+![]() ×7
×7![]() )=AD(BD+7)
)=AD(BD+7)
=ADBD+7AD=AD(14﹣AD)+7AD=﹣AD2+21AD=﹣(AD﹣![]() )2+
)2+![]() ,
,
∴当AD=![]() 时,
时,![]() 的最大值为
的最大值为![]() ,
,
∵AD+BD=14,
∴BD=14﹣![]() =
=![]() ,
,
在Rt△ABD中,根据勾股定理得,AB=![]() ,
,
∴⊙O的半径为OA=![]() AB=
AB=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,![]() 是学生小金家附近的一块三角形绿化区的示意图;为增强体质,他每天早晨都沿着绿化区周边小路AB,BC,CA跑步(小路的宽度不计),观测得点B在点A的南偏东30°方向上,点C在点A的南偏东60°的方向上,点B在点C的北偏西75°方向上,AC间距离为400米.
是学生小金家附近的一块三角形绿化区的示意图;为增强体质,他每天早晨都沿着绿化区周边小路AB,BC,CA跑步(小路的宽度不计),观测得点B在点A的南偏东30°方向上,点C在点A的南偏东60°的方向上,点B在点C的北偏西75°方向上,AC间距离为400米.
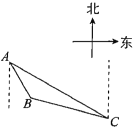
(1)求BC和AB;
(2)小金沿三角形绿化区的周边小路跑一圈共跑了多少米?(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
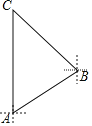
【题目】科技改变生活,导航装备的不断更新极大方便了人们的出行.如图,某校组织学生乘车到C地开展研学游活动,车到达A地后,发现C地恰好在A地的正北方向,且距离A地20千米,导航显示车辆应沿北偏东60°方向行驶至B地,再沿西北方向行驶一段距离才能到C地,求B、C两地的距离(计算结果用根号表示,不取近似值).
查看答案和解析>>
科目:初中数学 来源: 题型:
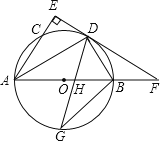
【题目】如图,AB是![]() 的直径,点C、D在
的直径,点C、D在![]() 上,且AD平分
上,且AD平分![]() ,过点D作AC的垂线,与AC的延长线相交于E,与AB的延长线相交于点F,G为AB的下半圆弧的中点,DG交AB于H,连接DB、GB.
,过点D作AC的垂线,与AC的延长线相交于E,与AB的延长线相交于点F,G为AB的下半圆弧的中点,DG交AB于H,连接DB、GB.
![]() 证明EF是
证明EF是![]() 的切线;
的切线;
![]() 求证:
求证:![]() ;
;
![]() 已知圆的半径
已知圆的半径![]() ,
,![]() ,求GH的长.
,求GH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某同学报名参加校运动会,有以下5个项目可供选择:径赛项目:100m,200m,![]() 分别用
分别用![]() 、
、![]() 、
、![]() 表示
表示![]() ;田赛项目:跳远,跳高
;田赛项目:跳远,跳高![]() 分别用
分别用![]() 、
、![]() 表示
表示![]() .
.
![]() 该同学从5个项目中任选一个,恰好是田赛项目的概率为______;
该同学从5个项目中任选一个,恰好是田赛项目的概率为______;
![]() 该同学从5个项目中任选两个,利用树状图或表格列举出所有可能出现的结果,并求恰好是一个田赛项目和一个径赛项目的概率.
该同学从5个项目中任选两个,利用树状图或表格列举出所有可能出现的结果,并求恰好是一个田赛项目和一个径赛项目的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
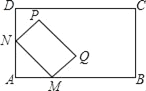
【题目】如图,将矩形MNPQ放置在矩形ABCD中,使点M,N分别在AB,AD边上滑动,若MN=6,PN=4,在滑动过程中,点A与点P的距离AP的最大值为( )
A. 4 B. 2![]() C. 7 D. 8
C. 7 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
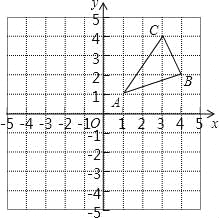
(1)请画出△ABC向左平移5个单位长度后得到的△A1B1C1;
(2)请画出△ABC关于原点对称的△A2B2C2;
(3)在x轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() .
.
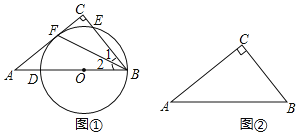
(1)如图①,点![]() 在斜边
在斜边![]() 上,以点
上,以点![]() 为圆心,
为圆心,![]() 长为半径的圆交
长为半径的圆交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,与边
,与边![]() 相切于点
相切于点![]() .求证:
.求证:![]() ;
;
(2)在图②中作![]() ,使它满足以下条件:
,使它满足以下条件:
①圆心在边![]() 上;②经过点
上;②经过点![]() ;③与边
;③与边![]() 相切.
相切.
(尺规作图,只保留作图痕迹,不要求写出作法)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,对角线AC的垂直平分线EF分别交BC,AD于点E,F,若BE=3,AF=5,则AC的长为( )

A. ![]() B.
B. ![]() C. 10D. 8
C. 10D. 8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com