
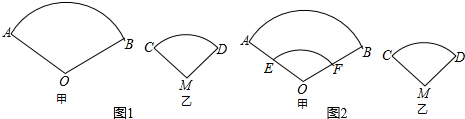
分析 (1)只需运用扇形的面积公式就可解决问题;
(2)只需运用(1)中的结果就可算出两个扇形用纸面积,通过比较就可解决问题;
(3)设乙扇形半径为r,圆心角为α,则甲扇形的半径为2r,圆心角为$\frac{1}{2}$α,然后只需运用扇形的面积公式就可解决问题.
解答 解:(1)如图1,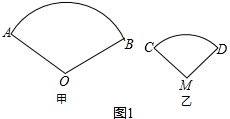
甲扇形所用纸的面积为2×$\frac{120π•O{A}^{2}}{360}$=2×$\frac{120×3×4{0}^{2}}{360}$=3200,
乙扇形所用纸的面积为2×$\frac{120πM{D}^{2}}{360}$=2×$\frac{120×3×2{0}^{2}}{360}$=800;
(2)如图2,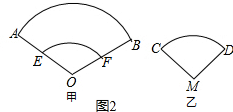
甲扇形所用纸的面积为3200-800=2400,乙扇形所用纸的面积为800,
∴甲扇形用纸面较大;
(3)设乙扇形半径为r,圆心角为α,则甲扇形的半径为2r,圆心角为$\frac{1}{2}$α,
∴S甲扇形=$\frac{\frac{1}{2}απ(2r)^{2}}{360}$=$\frac{πα{r}^{2}}{180}$,S乙扇形=$\frac{α•π•{r}^{2}}{360}$,
∴S甲扇形=2S乙扇形.
故答案为2.
点评 本题考查的是扇形面积公式的运用,其中半径为r,圆心角为n°的扇形的面积为$\frac{nπ{r}^{2}}{360}$;需要注意的是(1)中扇形两面都贴纸,扇形所用纸的面积应是扇形面积的2倍.


科目:初中数学 来源:2017届山东省日照市莒县第三协作区九年级3月学业水平模拟考试数学试卷(解析版) 题型:单选题
一个纸环链,纸环按红黄绿蓝紫的顺序重复排列,截去其中的一部分剩下部分如图所示,则被截去部分纸环的个数可能是( )

A. 2013 B. 2014 C. 2015 D. 2016
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com