
【题目】如图,在所给的正方形网格中,每个小正方形的边长均为1个单位,每个小正方形的顶点称为格点.格点△ABD中,A(-3,5)、B(-7,2)、D(0,2) .

(1) 作出□ABCD,并直接写出C点坐标为_______;
(2) 作出BD的中点M
(3) 在y轴上作出点N(不与点D重合),使得∠NAD=∠NBD.
【答案】(1)图见解析,![]() ;(2)图见解析;(3)图见解析.
;(2)图见解析;(3)图见解析.
【解析】
(1)分别过点B作AD的平行线、过点D作AB的平行线,两条平行线的交点即为点C;先根据平行四边形的性质可得点A平移到点D的平移方式与点B平移到点C的平移方式相同,再根据点A、D的坐标得出平移方式,由此即可得出点C的坐标;
(2)根据平行四边形的性质,连接AC,与BD的交点即为中点M;
(3)过点A作AB的垂线,与y轴的交点即为点N,理由:设BN的中点为点P,连接PA、PD,根据直角三角形的性质可得![]() ,再利用圆周角定理即可得证.
,再利用圆周角定理即可得证.
(1)分别过点B作AD的平行线、过点D作AB的平行线,两条平行线的交点即为点C,作图结果如下所示:

由平行四边形的性质可知,点A平移到点D的平移方式与点B平移到点C的平移方式相同
![]()
![]() 点A平移到点D的平移方式为:先向右平移3个单位长度,再向下平移3个单位长度
点A平移到点D的平移方式为:先向右平移3个单位长度,再向下平移3个单位长度
![]()
![]() 点C的坐标为
点C的坐标为![]() ,即
,即![]()
故答案为:![]() ;
;
(2)平行四边形的性质:对角线互相平分
连接AC,与BD的交点即为中点M,如图所示:

(3)如图,过点A作AB的垂线,与y轴的交点即为点N,理由如下:
设BN的中点为点P,连接PA、PD
![]() 点P为BN的中点
点P为BN的中点
![]() PA为
PA为![]() 斜边上的中线,PD为
斜边上的中线,PD为![]() 斜边上的中线
斜边上的中线
![]() ,
,![]()
![]()
则以点P为圆心,PA的长为半径画圆,一定经过点![]()
由圆周角定理得:![]() .
.



科目:初中数学 来源: 题型:
【题目】某公司组织退休职工组团前往某景点游览参观,参加人员共70人.旅游景点规定:①门票每人60元,无优惠;②上山游览必须乘坐景点安排的观光车游览,观光车有小型车和中型车两类,分别可供4名和11名乘客乘坐;且小型车每辆收费60元,中型车每人收费10元.若70人正好坐满每辆车且参观游览的总费用不超过5000元,问景点安排的小型车和中型车各多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
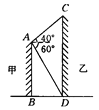
【题目】如图所示,两建筑物的水平距离为24 m,从A点测得D点的俯角为60°,测得C点的仰角为40°,求这两座建筑物的高.(![]() ≈1.732,tan 40°≈0.8391,精确到0.01 m)
≈1.732,tan 40°≈0.8391,精确到0.01 m)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究如图,直线![]() 的解析式为
的解析式为![]() ,且
,且![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 经过点
经过点![]() 和点
和点![]() ,直线
,直线![]() ,
,![]() 交于点
交于点![]() ,连接
,连接![]() .
.
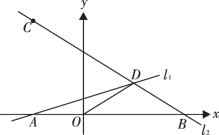
(1)求直线![]() 的解析式;
的解析式;
(2)求证:![]() 是等腰三角形;
是等腰三角形;
(3)求![]() 的面积;
的面积;
(4)探究在直线![]() 上是否存在异于点
上是否存在异于点![]() 的另一点
的另一点![]() ,使得
,使得![]() 与
与![]() 的面积相等,若存在,请直接写出点
的面积相等,若存在,请直接写出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把a、b、c三个数按照从小到大排列,中间的数记作MID{a,b,c},直线y=kx+2k(k>0)与函数y=MID{![]() ,2x+1,-x+2}的图象有且只有1个交点,则k的取值范围是______.
,2x+1,-x+2}的图象有且只有1个交点,则k的取值范围是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴上点![]() 对应的数分别是
对应的数分别是![]() 、
、![]() ,
,![]() 为数轴上两个动点,它们同时向右运动.点
为数轴上两个动点,它们同时向右运动.点![]() 从点
从点![]() 出发,速度为每秒
出发,速度为每秒![]() 个单位长度;点
个单位长度;点![]() 从点
从点![]() 出发,速度为点
出发,速度为点![]() 的
的![]() 倍,点
倍,点![]() 为原点.
为原点.
(1)当运动![]() 秒时,点
秒时,点![]() 对应的数分别是 、 .
对应的数分别是 、 .
(2)求运动多少秒时,点![]() 中恰有一个点为另外两个点所连线段的中点?
中恰有一个点为另外两个点所连线段的中点?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+3的对称轴是直线x=1.
(1)求证:2a+b=0;
(2)若关于x的方程ax2+bx﹣8=0的一个根为4,求方程的另一个根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一小球从斜坡D点处抛出,球的抛出路线可以用二次函数)y=-x2+4x刻画,斜坡OA可以用一次函数y=![]() 刻画.
刻画.
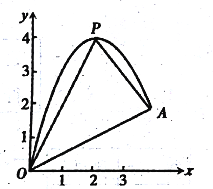
(1)请用配方法求二次函数图象的最高点P的坐标;
(2)小球的落点是A,求点A的坐标
(3)连接抛物线的最高点P与点O、A得△POA,求△POA的面积;
(4)在OA上方的抛物线上存在一点M(M与P不重合),△MOA的面积等于△POA的面积,请直接写出点M的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com