
【题目】数轴上点![]() 对应的数分别是
对应的数分别是![]() 、
、![]() ,
,![]() 为数轴上两个动点,它们同时向右运动.点
为数轴上两个动点,它们同时向右运动.点![]() 从点
从点![]() 出发,速度为每秒
出发,速度为每秒![]() 个单位长度;点
个单位长度;点![]() 从点
从点![]() 出发,速度为点
出发,速度为点![]() 的
的![]() 倍,点
倍,点![]() 为原点.
为原点.
(1)当运动![]() 秒时,点
秒时,点![]() 对应的数分别是 、 .
对应的数分别是 、 .
(2)求运动多少秒时,点![]() 中恰有一个点为另外两个点所连线段的中点?
中恰有一个点为另外两个点所连线段的中点?
【答案】(1)6+t;﹣12+3t;(2)1.5,6,24秒.
【解析】
(1)根据题意,利用路程=速度×时间表示出M与N表示的数即可;
(2)设运动t秒后,点M、N、O中恰有一个点为另两个点所连线段的中点,分三种情况考虑:O为MN中点;N为MO中点;M为NO中点,分别求出t的值即可.
(1)根据题意得:M表示的数为6+t,N表示的数为﹣12+3t.
故答案为:6+t;﹣12+3t; .
![]()
(2)设运动t秒后,点M、N、O恰有一个点为另两个点所连线段的中点,分三种情况讨论:
①若点O为MN的中点,则6+t=﹣(﹣12+3t),解得:t=1.5;
②当点N为MO的中点,则6+t=2(﹣12+3t),解得:t=6;
③当点M为NO的中点,则﹣12+3t=2(6+t),解得:t=24.
综上,运动1.5,6,24秒后,点M、N、O中恰有一个点为另两个点所连线段的中点.


 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:初中数学 来源: 题型:
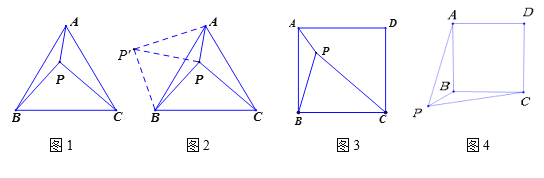
【题目】(问题提出)在数学“共生课堂”上,某合作小组提出了这样一个问题:如图1,在等边三角形ABC内有一点P,且PA=1,PB=2,PC=![]() .你能求出∠APB的度数吗?
.你能求出∠APB的度数吗?
(问题解决)(1)李清同学分析题目后,发现以PA、PB、PC的长为边的三角形是直角三角形,他找到了正确的思路:如图2,将△BPC绕点B逆时针旋转60°,得到△BP′A.连接PP′,易得△P′PB是等边三角形,△P′PA是直角三角形,则得∠BPP′=_________,∠APB=_________.
(问题类比)(2)同组的祁响同学突然想起曾经解决过的一个问题:如图3,点P是正方形ABCD内一点,PA=1,PB=2,PC=3.求∠APB的度数.请你写出解答过程.
(问题延伸)(3)夏老师留了一个思考题:如图4,若点P是正方形ABCD外一点,PA=![]() ,PB=1,PC=
,PB=1,PC=![]() .则∠APB的度数.请你写出解答过程.
.则∠APB的度数.请你写出解答过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示在平面直角坐标系中,方格纸中每个小方格都是边长为1个单位长度的正方形,已知点![]() ,
,![]() ,
,![]() .
.

(1)在所给的直角坐标系中画出三角形![]() ;
;
(2)把三角形![]() 向左平移3个单位,再向上平移2个单位得到三角形
向左平移3个单位,再向上平移2个单位得到三角形![]() ,画出三角形
,画出三角形![]() 并写出点
并写出点![]() 的坐标;
的坐标;
(3)求三角形![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了测量被池塘隔开的A,B两点之间的距离,根据实际情况,作出如图所示的图形,其中AB⊥BE,EF⊥BE,AF交BE于点D,C在BD上.有四位同学分别测量出以下4组数据:①BC,∠ACB;②CD,∠ACB,∠ADB;③EF,DE,BD;④DE,DC,BC.能根据所测数据,求出A,B两点之间距离的有( )
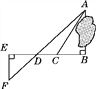
A. 1组 B. 2组 C. 3组 D. 4组
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在所给的正方形网格中,每个小正方形的边长均为1个单位,每个小正方形的顶点称为格点.格点△ABD中,A(-3,5)、B(-7,2)、D(0,2) .

(1) 作出□ABCD,并直接写出C点坐标为_______;
(2) 作出BD的中点M
(3) 在y轴上作出点N(不与点D重合),使得∠NAD=∠NBD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知动点P(t-6,![]() )在定直线l1上运动.
)在定直线l1上运动.

(1) 求直线l1的函数解析式;
(2) 如图1,l1与x轴交于点A,与y轴交于点B,点C与点A关于y轴对称,过点P作y轴的平行线,交x轴于点M,交直线BC于点Q;
① 若△PQB的面积为3,求点M的坐标;
② 如图2,连接BM.若∠BMP=∠BAC,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ,
,![]() ,
,![]() .说明:
.说明:![]() .请完成如下解答.
.请完成如下解答.

解:因为![]() (已知)
(已知)
所以![]() ( )
( )
因为![]() (已知)
(已知)
所以![]() ( )
( )
所以![]() ( )
( )
所以![]()
![]() ( )
( )
因为![]() (已知)
(已知)
所以![]() ( )
( )
所以![]() ( )
( )
所以![]() ( )
( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自2019年11月20日零时起,大西高铁车站开始试点电子客票业务,旅客购票乘车更加便捷.大西高铁客运专线是国家《中长期铁路网规划》中的重要组成部分,它的建成将意味着今后山西人去西安旅行的路程与时间将大大缩短,但也有不少游客根据自己的喜好依然选择乘坐普通列车.已知高铁线路中从A地到某市的高铁行驶路程是400km,普通列车的行驶路程是高铁行驶路程的1.3倍,若高铁的平均速度(km/h)是普通列车平均速度(km/h)的2.5倍,且乘坐高铁所需时间比乘坐普通列车所需时间缩短3.6h,求普通列车和高铁的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别为E,F.则下列结论:①AD上任意一点到点C,B的距离相等;②AD上任意一点到边AB,AC的距离相等;③BD=CD,AD⊥BC;④∠BDE=∠CDF.其中正确的个数为( )
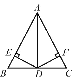
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com