
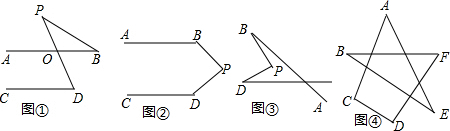
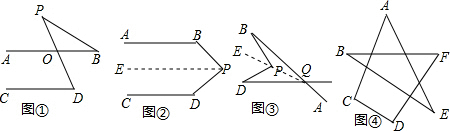
 解:(1)上述结论不成立.
解:(1)上述结论不成立.

 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
 某班同学在“献爱心”活动中捐了图书,捐书的情况如下:每人捐书的册数为:5,10,15,20,相应的捐书人数为:17,22,4,2.根据题目中所给的条件回答下列问题:
某班同学在“献爱心”活动中捐了图书,捐书的情况如下:每人捐书的册数为:5,10,15,20,相应的捐书人数为:17,22,4,2.根据题目中所给的条件回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:
| 上周末收盘价 | 周一 | 周二 | 周三 | 周四 | 周五 |
| 10.00 | +0.28 | -0.36 | +0.38 | -0.35 | +0.25 |
查看答案和解析>>
科目:初中数学 来源: 题型:
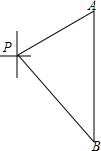 如图,一艘海轮位于灯塔P的北偏东60°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,这时,海轮所在的B处距离灯塔P有多远?(精确到0.01海里)
如图,一艘海轮位于灯塔P的北偏东60°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,这时,海轮所在的B处距离灯塔P有多远?(精确到0.01海里)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com