
已知:抛物线C1: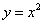 。如图(1),平移抛物线C1得到抛物线C2,C2经过C1的顶点O和A(2,0),C2的对称轴分别交C1、C2于点B、D。
。如图(1),平移抛物线C1得到抛物线C2,C2经过C1的顶点O和A(2,0),C2的对称轴分别交C1、C2于点B、D。
(1)求抛物线C2的解析式;
(2)探究四边形ODAB的形状并证明你的结论;
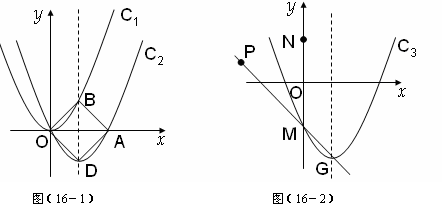
(3)如图(2),将抛物线C2向m个单位下平移(m>0)得抛物线C3,C3的顶点为G,与y轴交于M。点N是M关于x轴的对称点,点P(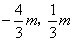 )在直线MG上。问:当m为何值时,在抛物线C3上存在点Q,使得以M、N、P、Q为顶点的四边形为平行四边形?
)在直线MG上。问:当m为何值时,在抛物线C3上存在点Q,使得以M、N、P、Q为顶点的四边形为平行四边形?

解:(1)设抛物线C2的解析式为 ,把A(2,0)代入得,
,把A(2,0)代入得, 。
。
 ∴抛物线C2的解析式为
∴抛物线C2的解析式为 。
。
(2)四边形ODAB是正方形,理由如下:
设BD与x轴交于点E,
∵ ,
,
∴D(1,-1),B(1,1),E(1,0)。
 ∴OE=EA=ED=EB=1,且OA⊥BD,
∴OE=EA=ED=EB=1,且OA⊥BD,
∴ODAB为正方形。
(3)设抛物线C3的解析式为 。
。
则M(0, ),N(0,
),N(0, ),
),
 ,∴G(1,
,∴G(1, )。
)。
设直线MG为 ,则
,则 ,
,
解得 ,
,
∴直线MG为 。
。
如图,若P、M、N、R四点构成平行四边形,
只能有三种情况,而显然R在第三象限不可能,
∴R只可能在四象限或二象限。
① 若R在第四象限,∵M、N关于点O对称,
所以P、R也关于点O对称,
∴R( ),
),
过N作NQ∥PM,
∴直线NQ为 ,
,
当 时,
时, ,
,
∴R在直线NR上。
把R( )代入
)代入 ,得
,得

∵ ,∴
,∴ 。
。
② 若R在第二象限,则PR∥MN,PM∥NR,,且R在NQ上
若R在第二象限,则PR∥MN,PM∥NR,,且R在NQ上
∵MN⊥x轴,∴PR⊥x轴,则R( )
)
∵R在NQ上,
∴ ,
,
又∵R在抛物线C3上,则
∵ ,∴
,∴ 。
。
∴当 或
或 时,在抛物线C3上存在点Q,使得以M、N、P、Q为顶点的
时,在抛物线C3上存在点Q,使得以M、N、P、Q为顶点的
四边形为平行四边形。


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
如图①,在正方形ABCD中,P是对角线AC上的一点,点E在BC的延长线上,且PE=PB.
(1)求证:△BCP≌△DCP;
(2)求证:∠DPE=∠ABC;
(3)把正方形ABCD改为菱形,其它条件不变(如图②),若∠ABC=58°,则∠DPE= 度.

查看答案和解析>>
科目:初中数学 来源: 题型:
观察下面的表格.
|
| 0 | 1 | 2 |
|
| 1 | ||
|
| -3 | -3 |
(1) 求a、b、c的值
(2) 设y=ax2+bx+c,求这个二次函数图象的对称轴和图象与x轴的交点坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com