
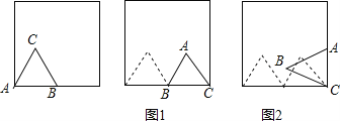
ЎҫМвДҝЎҝИзНјЈ¬ұЯіӨОӘ1өДХэИэҪЗРОABC·ЕЦГФЪұЯіӨОӘ2өДХэ·ҪРОДЪІҝЈ¬¶ҘөгAФЪХэ·ҪРОөДТ»ёц¶ҘөгЙПЈ¬ұЯABФЪХэ·ҪРОөДТ»ұЯЙПЈ¬Ҫ«ЎчABCИЖөгBЛіКұХлРэЧӘЈ¬өұөгCВдФЪХэ·ҪРОөДұЯЙПКұЈ¬НкіЙөЪ1ҙООЮ»¬¶Ҝ№ц¶ҜЈЁИзНј1Ј©Ј»ФЩҪ«ЎчABCИЖөгCЛіКұХлРэЧӘЈ¬өұөгAВдФЪХэ·ҪРОөДұЯЙПКұЈ¬НкіЙөЪ2ҙООЮ»¬¶Ҝ№ц¶ҜЈЁИзНј2Ј©Ј¬ЎӯЈ¬ГҝҙОРэЧӘөДҪЗ¶И¶јІ»ҙуУЪ120ЎгЈ¬ТАҙОХвСщІЩЧчПВИҘЈ¬өұНкіЙөЪ2016ҙООЮ»¬¶Ҝ№ц¶ҜКұЈ¬өгAҫӯ№эөДВ·ҫ¶ЧЬіӨОӘ ______Ј®
Ўҫҙр°ёЎҝ560ҰРЈ®
ЎҫҪвОцЎҝ
ПИЗуіцөЪТ»ҙОөҪөЪБщҙОРэЧӘөДВ·ҫ¶өДіӨ·ЦұрКЗ¶аЙЩЈ¬МҪҫҝ№жВЙәујҙҝЙҪвҫцОКМвЈ®
өЪТ»ҙОРэЧӘөДВ·ҫ¶іӨОӘ![]() =
=![]() ҰРЈ¬
ҰРЈ¬
өЪ¶юҙОРэЧӘөДВ·ҫ¶іӨОӘ![]() =
=![]() ҰРЈ¬
ҰРЈ¬
өЪИэҙОРэЧӘөДВ·ҫ¶іӨОӘ0Ј¬
өЪЛДҙОРэЧӘөДВ·ҫ¶іӨОӘ![]() ҰРЈ¬
ҰРЈ¬
өЪОеҙОРэЧӘөДВ·ҫ¶іӨОӘ![]() ҰРЈ¬
ҰРЈ¬
өЪБщҙОРэЧӘөДВ·ҫ¶іӨОӘ0Ј¬
Ўӯ
УЙҙЛ·ўПЦГҝИэҙОРэЧӘөДВ·ҫ¶әНОӘ![]() ҰР+
ҰР+![]() ҰР=
ҰР=![]() ҰРЈ®
ҰРЈ®
2016ЎВ3=672Ј¬
ЎаНкіЙөЪ2016ҙООЮ»¬¶Ҝ№ц¶ҜКұЈ¬өгAҫӯ№эөДВ·ҫ¶ЧЬіӨОӘ672ЎБ![]() ҰР=560ҰРЈ®
ҰР=560ҰРЈ®
№Кҙр°ёОӘ560ҰРЈ®


 И«УЕіеҙМ100·ЦПөБРҙр°ё
И«УЕіеҙМ100·ЦПөБРҙр°ё УўІЕөгҪтПөБРҙр°ё
УўІЕөгҪтПөБРҙр°ё
| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
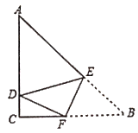
ЎҫМвДҝЎҝИзНјЈ¬ФЪ![]() ЦРЈ¬
ЦРЈ¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() ·ЦұрОӘ
·ЦұрОӘ![]() Ўў
Ўў![]() ЙПөДөгЈ¬СШЦұПЯ
ЙПөДөгЈ¬СШЦұПЯ![]() Ҫ«
Ҫ«![]() ХЫөюЈ¬К№өгBЗЎәГВдФЪ
ХЫөюЈ¬К№өгBЗЎәГВдФЪ![]() ЙПөД
ЙПөД![]() ҙҰЈ¬өұ
ҙҰЈ¬өұ![]() ЗЎәГОӘЦұҪЗИэҪЗРОКұЈ¬
ЗЎәГОӘЦұҪЗИэҪЗРОКұЈ¬![]() өДіӨОӘ__________Ј®
өДіӨОӘ__________Ј®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝФЪЖҪГжЦұҪЗЧшұкПөЦРЈ¬өгAөДЧшұкОӘЈЁ4Ј¬0Ј©Ј¬өгBОӘyЦбЙПөДТ»¶ҜөгЈ¬Ҫ«ПЯ¶ОABИЖөгBЛіКұХлРэЧӘ90ЎгөГПЯ¶ОBCЈ¬ИфөгCЗЎәГВдФЪ·ҙұИАэәҜКэyЈҪ![]() өДНјПуЙПЈ¬ФтөгBөДЧшұкОӘ_____Ј®
өДНјПуЙПЈ¬ФтөгBөДЧшұкОӘ_____Ј®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘЎчABCКЗөИұЯИэҪЗРОЈ¬өгPКЗЖҪГжДЪТ»өгЈ¬ЗТЛДұЯРОPBCDОӘЖҪРРЛДұЯРОЈ¬Ҫ«ПЯ¶ОCDИЖөгCДжКұХлРэЧӘ60ЎгЈ¬өГөҪПЯ¶ОCF
(1)ИзНј1Ј¬өұPОӘACөДЦРөгКұЈ¬ЗуЦӨЈәFCЎНPD.
(2)ИзНј2Ј¬өұPОӘЎчABCДЪИОТ»өгКұЈ¬Б¬ҪУPAЎўPFЎўAFЈ¬КФЕР¶ПЎчPAFөДРОЧҙЈ¬ІўЦӨГчДгөДҪбВЫ.
(3)өұBЎўPЎўFИэөг№ІПЯЗТAB=![]() Ј¬PB=3КұЈ¬ЗуPAөДіӨ.
Ј¬PB=3КұЈ¬ЗуPAөДіӨ.

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝ ИзНјЈ¬ЖҪГжЦұҪЗЧшұкПөЦРЈ¬ҫШРОOABCөД¶ҘөгBөДЧшұкОӘЈЁ7Ј¬5Ј©Ј¬¶ҘөгAЈ¬C·ЦұрФЪxЦбЈ¬yЦбЙПЈ¬өгDөДЧшұкОӘЈЁ0Ј¬1Ј©Ј¬№эөгDөДЦұПЯУлҫШРОOABCөДұЯBCҪ»УЪөгGЈ¬ЗТөгGІ»УлөгCЦШәПЈ¬ТФDGОӘТ»ұЯЧчБвРОDEFGЈ¬өгEФЪҫШРОOABCөДұЯOAЙПЈ¬ЙиЦұПЯDGөДәҜКэұнҙпКҪОӘy=kx+b
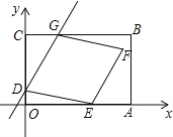
ЈЁ1Ј©өұCG=ODКұЈ¬ЗуЦұПЯDGөДәҜКэұнҙпКҪЈ»
ЈЁ2Ј©өұөгEөДЧшұкОӘЈЁ5Ј¬0Ј©КұЈ¬ЗуЦұПЯDGөДәҜКэұнҙпКҪЈ»
ЈЁ3Ј©Б¬ҪУBFЈ¬ЙиЎчFBGөДГж»эОӘSЈ¬CGөДіӨОӘaЈ¬ЗлЦұҪУРҙіцSУлaөДәҜКэұнҙпКҪј°ЧФұдБҝaөДИЎЦө·¶О§Ј®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬Т»ҙОәҜКэy=x+3УлЧшұкЦбҪ»УЪAЎўCБҪөгЈ¬№эAЎўCБҪөгөДЕЧОпПЯy=ax2-2x+cУлxЦбҪ»УЪБнТ»өгBЕЧОпПЯ¶ҘөгОӘEЈ¬Б¬ҪУAEЈ®
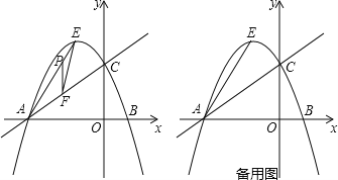
ЈЁ1Ј©ЗуёГЕЧОпПЯөДәҜКэұнҙпКҪј°¶ҘөгEЧшұкЈ»
ЈЁ2Ј©өгPКЗПЯ¶ОAEЙПөДТ»¶ҜөгЈ¬№эөгPЧчPFЖҪРРУЪyЦбҪ»ACУЪөгBБ¬ҪУEFЈ¬ЗуЎчPEFГж»эөДЧоҙуЦөј°ҙЛКұөгPөДЧшұкЈ»
ЈЁ3Ј©ИфөгMОӘЧшұкЦбЙПТ»өгЈ¬өгNОӘЖҪГжДЪИОТвТ»өгЈ¬КЗ·сҙжФЪХвСщөДөгЈ¬К№AЎўEЎўMЎўNОӘ¶ҘөгөДЛДұЯРОКЗТФAEОӘ¶ФҪЗПЯөДҫШРОЈҝИз№ыҙжФЪЈ¬ЗлЦұҪУРҙіцNөгЧшұкЈ»ИфІ»ҙжФЪЈ¬ЗлЛөГчАнУЙЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘmЈ¬n·ЦұрКЗ№ШУЪxөДТ»ФӘ¶юҙО·ҪіМax2+bx+cЈҪaУлax2+bx+cЈҪbөДТ»ёцёщЈ¬ЗТmЈҪn+1Ј®
(1)өұmЈҪ2Ј¬aЈҪ©Ғ1КұЈ¬ЗуbУлcөДЦөЈ»
(2)УГЦ»ә¬ЧЦДёaЈ¬nөДҙъКэКҪұнКҫbЈ»
(3)өұaЈј0КұЈ¬әҜКэyЈҪax2+bx+cВъЧгb2©Ғ4acЈҪaЈ¬b+cЎЭ2aЈ¬nЎЬ©Ғ![]() Ј¬ЗуaөДИЎЦө·¶О§Ј®
Ј¬ЗуaөДИЎЦө·¶О§Ј®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
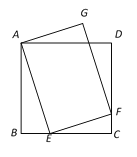
ЎҫМвДҝЎҝИзНјЈ¬ТСЦӘХэ·ҪРОABCDЦРЈ¬өгEКЗBCЙПөДТ»ёц¶ҜөгЈ¬EFЎНAEҪ»CDУЪөгFЈ¬ТФAEЈ¬EFОӘұЯЧчҫШРОAEFGЈ¬ИфAB=4Ј¬ФтөгGөҪADҫаАлөДЧоҙуЦөКЗ________.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
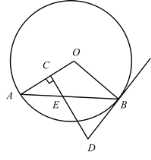
ЎҫМвДҝЎҝИзНјЈ¬![]() КЗ
КЗ![]() өДПТЈ¬№э
өДПТЈ¬№э![]() өДЦРөг
өДЦРөг![]() Чч
Чч![]() Ј¬ҙ№ЧгОӘ
Ј¬ҙ№ЧгОӘ![]() Ј¬№эөг
Ј¬№эөг![]() Чч
Чч![]() өДЗРПЯ
өДЗРПЯ![]() Ҫ»
Ҫ»![]() өДСУіӨПЯУЪөг
өДСУіӨПЯУЪөг![]() Ј®
Ј®
ЈЁ1Ј©ЗуЦӨЈә![]() Ј»
Ј»
ЈЁ2Ј©Б¬ҪУ![]() Ј¬Иф
Ј¬Иф![]() Ј¬
Ј¬![]() Ј¬ЗуЛДұЯРО
Ј¬ЗуЛДұЯРО![]() өДГж»эЈ®
өДГж»эЈ®
Ійҝҙҙр°ёәНҪвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com