
【题目】如图,![]() 是
是![]() 的弦,过
的弦,过![]() 的中点
的中点![]() 作
作![]() ,垂足为
,垂足为![]() ,过点
,过点![]() 作
作![]() 的切线
的切线![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
(1)求证:![]() ;
;
(2)连接![]() ,若
,若![]() ,
,![]() ,求四边形
,求四边形![]() 的面积.
的面积.
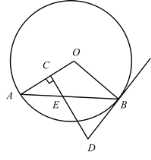
【答案】(1)见解析;(2)204
【解析】
(1)要证明DB=DE,只要证明∠DEB=∠DBE即可;
(2)作DF⊥AB于F,连接OE.只要证明∠AOE=∠DEF,可得sin∠DEF=sin∠AOE=![]() ,由此求出AO的长,由勾股定理可求OE的长即可解决问题.
,由此求出AO的长,由勾股定理可求OE的长即可解决问题.
证明:(1)∵AO=OB,
∴∠OAB=∠OBA,
∵BD是切线,
∴OB⊥BD,
∴∠OBD=90°,
∴∠OBE+∠EBD=90°,
∵EC⊥OA,
∴∠CAE+∠CEA=90°,
∵∠CEA=∠DEB,
∴∠EBD=∠BED,
∴DB=DE.
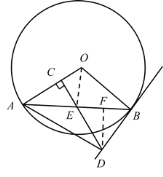
(2)作DF⊥AB于F,连接OE.
∵DB=DE,AE=EB=![]() AB=12,
AB=12,
∴EF=![]() BE=6,OE⊥AB,
BE=6,OE⊥AB,
在Rt△EDF中,DE=BD=10,EF=6,
∴DF=![]() ,
,
∵∠AOE+∠OAB=90°,∠DEF+∠OAB=90°,
∴∠AOE=∠DEF,
∴sin∠DEF=sin∠AOE=![]() ,
,
∵AE=12,
∴AO=15
∴OE=![]()
∴四边形OADB的面积=![]() ×AB×OE+
×AB×OE+![]() ×AB×DF=204.
×AB×DF=204.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:
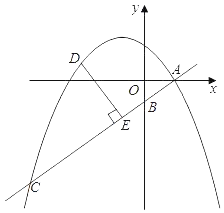
【题目】如图,在平面直角坐标系中,直线y=kx﹣![]() 与抛物线y=ax2+bx+
与抛物线y=ax2+bx+![]() 交于点A、C,与y轴交于点B,点A的坐标为(2,0),点C的横坐标为﹣8.
交于点A、C,与y轴交于点B,点A的坐标为(2,0),点C的横坐标为﹣8.
(1)请直接写出直线和抛物线的解析式;
(2)点D是直线AB上方的抛物线上一动点(不与点A、C重合),作DE⊥AC于点E.设点D的横坐标为m.求DE的长关于m的函数解析式,并写出DE长的最大值;
(3)平移△AOB,使平移后的三角形的三个顶点中有两个在抛物线上,请直接写出平移后的点A对应点A′的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
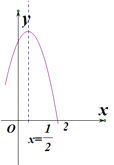
【题目】如图是二次函数![]() 图象的一部分,对称轴为
图象的一部分,对称轴为![]() ,且经过点
,且经过点![]() ,有下列说法:①
,有下列说法:①![]() ;②
;②![]() ;③
;③![]() ;④若
;④若![]() 是抛物线上的两点,则
是抛物线上的两点,则![]() ,上述说法正确的是( )
,上述说法正确的是( )
A.①②④B.③④C.①③④D.①②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD,点M是边BA延长线上的动点(不与点A重合),且AM<AB,△CBE由△DAM平移得到.若过点E作EH⊥AC,H为垂足,则有以下结论:①点M位置变化,使得∠DHC=60°时,2BE=DM;②无论点M运动到何处,都有DM=![]() HM;③无论点M运动到何处,∠CHM一定大于135°.其中正确结论的序号为_____.
HM;③无论点M运动到何处,∠CHM一定大于135°.其中正确结论的序号为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将抛物线M:y=- ![]() x2+2向左平移2个单位,再向上平移1个单位,得到抛物线M'.若抛物线M'与x轴交于A、B两点,M'的顶点记为C,则∠ACB=( )
x2+2向左平移2个单位,再向上平移1个单位,得到抛物线M'.若抛物线M'与x轴交于A、B两点,M'的顶点记为C,则∠ACB=( )
A.45°B.60°C.90°D.120°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,△AOB是等腰直角三角形,∠AOB=90°,点A(2,1).
(1)求点B的坐标;
(2)求经过A、O、B三点的抛物线的函数表达式;
(3)在(2)所求的抛物线上,是否存在一点P,使四边形ABOP的面积最大?若存在,求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平整的桌面上面一条直线l,将三边都不相等的三角形纸片ABC平放在桌面上,使AC与边l对齐,此时△ABC的内心是点P;将纸片绕点C顺时针旋转,使点B落在l上的点B'处,点A落在A'处,得到△A'B'C'的内心点P'.下列结论正确的是( )
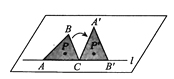
A.PP'与l平行,PC与P'B'平行
B.PP'与l平行,PC与P'B'不平行
C.PP'与l不平行,PC与P'B'平行
D.PP'与l不平行,PC与P'B'不平行
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com