
 如图,在四边形ABCD中,AB=4,CD=13,DE=12,∠DAB=∠DEC=90°,∠ABE=135°,四边形ABCD的面积是( )
如图,在四边形ABCD中,AB=4,CD=13,DE=12,∠DAB=∠DEC=90°,∠ABE=135°,四边形ABCD的面积是( )| A、94 | B、90 | C、84 | D、78 |
| 2 |
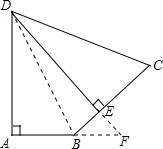 解:连接DB,延长AB和DE交于F,设BE=x,
解:连接DB,延长AB和DE交于F,设BE=x,| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
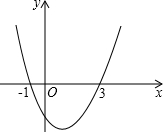 二次函数y=ax2+bx+c的图象如图所示,则下列说法中正确的是( )
二次函数y=ax2+bx+c的图象如图所示,则下列说法中正确的是( )| A、ac>0 |
| B、4a+2b+c>0 |
| C、当x>1时,y随x的增大而减小 |
| D、a+b<m(am+b)(m≠1) |
查看答案和解析>>
科目:初中数学 来源: 题型:
 九年级(1)班和(2)班各选派了七位学生参加一次科普知识竞赛,他们的成绩分别如下表:
九年级(1)班和(2)班各选派了七位学生参加一次科普知识竞赛,他们的成绩分别如下表:| 九(1)班 | 58 | 65 | 70 | 70 | 70 | 75 | 82 |
| 九(2)班 | 50 | 55 | 69 | 76 | 76 | 82 | 82 |
| 1 |
| n |
. |
| x |
. |
| x |
. |
| x |
. |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,AD是⊙O的直径,BC与⊙O相切于点B,连结AB、OB、BD,若∠ABC=65°,∠ADB等于( )
如图,AD是⊙O的直径,BC与⊙O相切于点B,连结AB、OB、BD,若∠ABC=65°,∠ADB等于( )| A、50° | B、55° |
| C、60° | D、65° |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| x |
A、-
| ||
B、0<x<
| ||
C、
| ||
D、1<x<
|
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在矩形ABCD中,AB=2,AD=4,将矩形ABCD沿直线EF折叠,D到G得位置,C到H得位置,BC交EG于M点.则图中四边形ABME和四边形GHFM的周长和是( )
如图,在矩形ABCD中,AB=2,AD=4,将矩形ABCD沿直线EF折叠,D到G得位置,C到H得位置,BC交EG于M点.则图中四边形ABME和四边形GHFM的周长和是( )A、4
| ||
B、8
| ||
| C、10 | ||
| D、12 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com