
分析 (1)方程组利用加减消元法求出解即可;
(2)方程组利用加减消元法求出解即可;
(3)方程组整理后,利用加减消元法求出解即可;
(4)方程组整理后,利用加减消元法求出解即可.
解答 解:(1)$\left\{\begin{array}{l}{2x-y=-5①}\\{3x+y=10②}\end{array}\right.$,
①+②得:5x=5,即x=1,
把x=1代入①得:y=7,
则方程组的解为$\left\{\begin{array}{l}{x=1}\\{y=7}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{2x+3y+z=6①}\\{x-y+2z=-1②}\\{x+2y-z=5③}\end{array}\right.$,
①+③得:3x+5y=11④,
②+③×2得:x+y=3⑤,
⑤×5-④得:2x=4,即x=2,
把x=2代入⑤得:y=1,
把x=2,y=1代入①得:z=-1,
则方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=1}\\{z=-1}\end{array}\right.$;
(3)方程组整理得:$\left\{\begin{array}{l}{x+2y=16①}\\{3x-2y=16②}\end{array}\right.$,
①+②得:4x=32,即x=8,
把x=8代入①得:y=4,
则方程组的解为$\left\{\begin{array}{l}{x=8}\\{y=4}\end{array}\right.$;
(4)方程组整理得:$\left\{\begin{array}{l}{3x-2y=2①}\\{x+y=9②}\end{array}\right.$,
①+②×2得:5x=20,即x=4,
把x=4代入②得:y=5,
则方程组的解为$\left\{\begin{array}{l}{x=4}\\{y=5}\end{array}\right.$.
点评 此题考查了解二元一次方程组,以及三元一次方程组,熟练掌握运算法则是解本题的关键.


 灵星计算小达人系列答案
灵星计算小达人系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
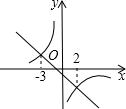 定义运算max{a,b}:当a≥b时,max{a,b}=a;当a<b时,max{a,b}=b.如max{-3,2}=2.
定义运算max{a,b}:当a≥b时,max{a,b}=a;当a<b时,max{a,b}=b.如max{-3,2}=2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
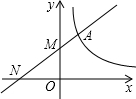 如图,一次函数y=kx+2与反比例函数y=$\frac{4}{x}$(x>0)的图象交于点A,与y轴交于点M,与x轴交于点N,且AM:MN=1:2,则k=$\frac{3}{4}$.
如图,一次函数y=kx+2与反比例函数y=$\frac{4}{x}$(x>0)的图象交于点A,与y轴交于点M,与x轴交于点N,且AM:MN=1:2,则k=$\frac{3}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com