练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

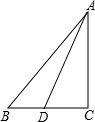
    如图，在△ABC中，AD=15，AC=12，DC=9，点B是CD延长线上一点，连接AB，若AB=20．求：△ABD的面积．


    【考点】勾股定理；勾股定理的逆定理．

    【分析】由勾股定理的逆定理证明△ADC是直角三角形，∠C=90°，再由勾股定理求出BC，得出BD，即可得出结果．

    【解答】解：在△ADC中，AD=15，AC=12，DC=9，

    AC2+DC2=122+92=152=AD2，

    即AC2+DC2=AD2，

    ∴△ADC是直角三角形，∠C=90°，

    在Rt△ABC中，BC===16，

    ∴BD=BC﹣DC=16﹣9=7，

    ∴△ABD的面积=×7×12=42．

    【点评】本题考查了勾股定理、勾股定理的逆定理；熟练掌握勾股定理，由勾股定理的逆定理证明三角形是直角三角形是解决问题的关键．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    某地为提倡节约用水，准备实行自来水“阶梯计费”方式，用户用水不超出基本用水量的部分享受基本价格，超出基本用水量的部分实行加价收费，为更好地决策，自来水公司随机抽取部分用户的用水量数据，并绘制了如下不完整统计图（每组数据包括右端点但不包括左端点），请你根据统计图解决下列问题：

    （1）此次调查抽取了多少用户的用水量数据？

    （2）补全频数分布直方图，求扇形统计图中“25吨～30吨”部分的圆心角度数；

    （3）如果自来水公司将基本用水量定为每户25吨，那么该地20万用户中约有多少用户的用水全部享受基本价格？

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知等腰三角形的一边长为4，另一边长为8，则这个等腰三角形的周长为__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知直线a∥y轴且与y轴的距离等于3，则直线a与x轴交点的坐标为__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    一个多边形的内角和是1260°，这个多边形的边数是(     )

    A．7       B．8       C．9       D．10

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在△ABC中，∠A=30°，若∠B=∠C，则∠B的度数是__________度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


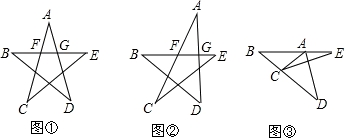
    探究：中华人民共和国国旗上的五角星的每个角均相等，小明为了计算每个角的度数，画出了如图①的五角星，每个角均相等，并写出了如下不完整的计算过程，请你将过程补充完整．

    解：∵∠AFG=∠C+∠E，∠AGF=∠B+∠D．

    ∴∠AFG+∠AGF=∠C+∠E+∠B+∠D．

    ∵∠A+∠AFG+∠AGF=__________°，

    ∴∠A+∠B+∠C+∠D+∠E=__________°，

    ∴∠A=∠B=∠C=∠D=∠E=__________°．

    拓展：如图②，小明改变了这个五角星的五个角的度数，使它们均不相等，请你帮助小明求∠A、∠B、∠C、∠D、∠E的和．

    应用：如图③．小明将图②中的点A落在BE上，点C落在BD上，若∠B=∠D=36°，则∠CAD+∠ACE+∠E=__________°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


     的相反数是         ，绝对值是           

    查看答案和解析>>

    同步练习册答案