
【题目】已知O是坐标原点,点A的坐标是(5,0),点B是y轴正半轴上一动点,以OB、OA为边作矩形OBCA,点E、H分别在边BC和边OA上,将△BOE沿着OE对折,使点B落在OC上的F点处,将△ACH沿着CH对折,使点A落在OC上的G点处.
(1)如图1,求证:四边形OECH是平行四边形;
(2)如图2,当点B运动到使得点F、G重合时,求点B的坐标,并判断四边形OECH是什么四边形?说明理由;
(3)当点B运动到使得点F,G将对角线OC三等分时,如图3,如图4,分别求点B的坐标.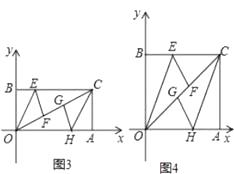
【答案】
(1)证明:如图1,
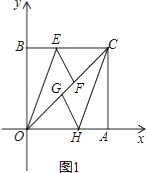
∵四边形OBCA为矩形,
∴OB∥CA,BC∥OA,
∴∠BOC=∠OCA,
又∵△BOE沿着OE对折,使点B落在OC上的F点处;△ACH沿着CH对折,使点A落在OC上的G点处,
∴∠BOC=2∠EOC,∠OCA=2∠OCH,
∴∠EOC=∠OCH,
∴OE∥CH,
又∵BC∥OA,
∴四边形OECH是平行四边形;
(2)解:点B的坐标是(0, ![]() );四边形OECH是菱形.理由如下:如图2,
);四边形OECH是菱形.理由如下:如图2,
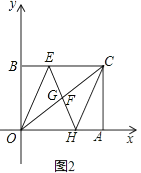
∵△BOE沿着OE对折,使点B落在OC上的F点处;△ACH沿着CH对折,使点A落在OC上的G点处,
∴∠EFO=∠EBO=90°,∠CFH=∠CAF=90°,
∵点F,G重合,
∴EH⊥OC,
又∵四边形OECH是平行四边形,
∴平行四边形OECH是菱形,
∴EO=EC,
∴∠EOC=∠ECO,
又∵∠EOC=∠BOE,
∴∠EOB=∠EOC=∠ECO=30°,
又∵点A的坐标是(5,0),
∴OA=5,
∴BC=5,
在Rt△OBC中,OB= ![]() BC=
BC= ![]() ,
,
∴点B的坐标是(0, ![]() );
);
(3)解:①当点F在点O,G之间时,如图3,
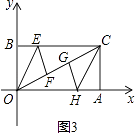
∵△BOE沿着OE对折,使点B落在OC上的F点处;△ACH沿着CH对折,使点A落在OC上的G点处,
∴OF=OB,CG=CA,
而OB=CA,
∴OF=CG,
∵点F,G将对角线OC三等分,
∴AC=OF=FG=GC,
设AC=m,则OC=3m,
在Rt△OAC中,OA=5,
∵AC2+OA2=OC2,
∴m2+52=(3m)2,解得m= ![]() ,
,
∴OB=AC= ![]() ,
,
∴点B的坐标是(0, ![]() );
);
②当点G在O,F之间时,如图4,
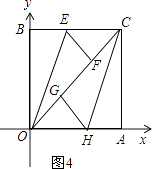
同理可得OF=CG=AC,
设OG=n,则AC=GC=2n,
在Rt△OAC中,OA=5,
∵AC2+OA2=OC2,
∴(2n)2+52=(3n)2,解得n= ![]() ,
,
∴AC=OB=2 ![]() ,
,
∴点B的坐标是(0,2 ![]() ).
).
【解析】(1)如图1,根据矩形的性质得OB∥CA,BC∥OA,再利用平行线的性质得∠BOC=∠OCA,然后根据折叠的性质得到∠BOC=2∠EOC,∠OCA=2∠OCH,故∠EOC=∠OCH,根据平行线的判定定理得OE∥CH,又BC∥OA,于是可根据平行四边形的判定方法得四边形OECH是平行四边形;
(2)如图2,先根据折叠的性质得∠EFO=∠EBO=90°,∠CFH=∠CAF=90°,由点F,G重合得到EH⊥OC,根据菱形的判定方法得到平行四边形OECH是菱形,则EO=EC,根据等边对等角得∠EOC=∠ECO,而∠EOC=∠BOE,根据三角形内角和定理可计算出∠EOB=∠EOC=∠ECO=30°,在Rt△OBC中,根据含30度的直角三角形三边的关系得OB ,从而得出B点的坐标;
(3)分类讨论:①当点F在点O,G之间时,如图3,,根据折叠的性质得OF=OB,CG=CA,则OF=CG,故AC=OF=FG=GC,设AC=m,则OC=3m,在Rt△OAC中,根据勾股定理得出方程,解方程得m的值,从而找到OA=AC的长,得出B点坐标;
②当点G在O,F之间时,如图4,,同理可得OF=CG=AC,设OG=n,则AC=GC=2n,在Rt△OAC中,OA=5,根据勾股定理得出方程,解出方程即得出AC=OB的长,进而得出B点的坐标。
【考点精析】解答此题的关键在于理解平行线的判定与性质的相关知识,掌握由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质,以及对平行四边形的判定的理解,了解两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,∠ABC=30°,AC=2,△ABC绕点C顺时针旋转得△A1B1C,当A1落在AB边上时,连接B1B,取BB1的中点D,连接A1D,则A1D的长度是( ) 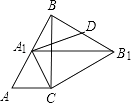
A.![]()
B.2 ![]()
C.3
D.2 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,△ABC三个顶点的坐标分别为A(﹣2,﹣1),B(﹣4,1),C(﹣3,3).△ABC关于原点O对称的图形是△A1B1C1 . 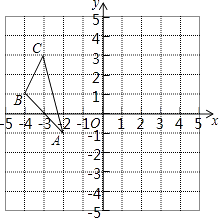
(1)画出△A1B1C1;
(2)BC与B1C1的位置关系是 , AA1的长为;
(3)若点P(a,b)是△ABC 一边上的任意一点,则点P经过上述变换后的对应点P1的坐标可表示为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】看图填空,并在括号内说明理由:
∵BD平分∠ABC(已知)
∴__________=__________(__________)
又∠1=∠D(已知)
∴__________=__________(__________)
∴__________∥__________(__________)
∴∠ABC+__________=180°(__________)
又∠ABC=55°(已知)
∴∠BCD=__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索:小明在研究数学问题:已知AB∥CD,AB和CD都不经过点P,探索∠P与∠C的数量关系.

发现:在如图中,:∠APC=∠A+∠C;如图
小明是这样证明的:过点P作PQ∥AB
∴∠APQ=∠A(_ __)
∵PQ∥AB,AB∥CD.
∴PQ∥CD(__ _)
∴∠CPQ=∠C
∴∠APQ+∠CPQ=∠A+∠C
即∠APC=∠A+∠C
(1)为小明的证明填上推理的依据;
(2)应用:①在如图中,∠P与∠A、∠C的数量关系为__ _;
②在如图中,若∠A=30![]() ,∠C=70
,∠C=70![]() ,则∠P的度数为__ _;
,则∠P的度数为__ _;
(3)拓展:在如图中,探究∠P与∠A,∠C的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线 AB、CD 相交于 O,∠BOC=70°,OE 是∠BOC 的角平分线,OF是OE的反向延长线.
(1)求∠1,∠2,∠3 的度数;
(2)判断 OF 是否平分∠AOD,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】夏季空调销售供不应求,某空调厂接到一份紧急订单,要求在10天内(含10天)完成任务,为提高生产效率,工厂加班加点,接到任务的第一天就生产了空调42台,以后每天生产的空调都比前一天多2台,由于机器损耗等原因,当日生产的空调数量达到50台后,每多生产一台,当天生产的所有空调,平均每台成本就增加20元.
(1)设第x天生产空调y台,直接写出y与x之间的函数解析式,并写出自变量x的取值范围.
(2)若每台空调的成本价(日生产量不超过50台时)为2000元,订购价格为每台2920元,设第x天的利润为W元,试求W与x之间的函数解析式,并求工厂哪一天获得的利润最大,最大利润是多少.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com