

分析 (1)先证明△ABP≌△DCQ,由此推出∠MPE=∠NQF,再证明△MEP≌△NFQ即可.
(2)分别在Rt△ABP,和Rt△MEP中,求出PB、PE即可解决问题.
(3)分别在Rt△ABP,和Rt△NPQ中,求出PB、PQ即可解决问题.
解答 解:(1)如图1中,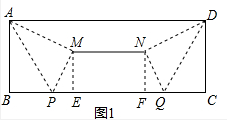
∵四边形ABCD是矩形,
∴∠B=∠C=90°,AB=CD,
在△ABP和△DCQ中,
$\left\{\begin{array}{l}{AB=DC}\\{∠B=∠C}\\{BP=CQ}\end{array}\right.$,
∴△ABP≌△DCQ.
∴∠APB=∠DQC,
由题意可知∠APB=∠APM,∠DQC=∠DQN,PB=PM=CQ=QN,
∴∠BPM=∠CQN,
∴∠MPE=∠NQF,
在△MEP和△NFQ中,
$\left\{\begin{array}{l}{∠MEP=∠NFQ=90°}\\{∠MPE=∠NQF}\\{PM=NQ}\end{array}\right.$,
∴△MEP≌△NFQ,
∴ME=NF.
(2)如图1中,在Rt△ABP中,∵∠B=90°,AB=6,∠APB=60°,
∴PB=AB•tan30°=2$\sqrt{3}$,
在Rt△PME中,∵PM=2$\sqrt{3}$,∠MEP=90°,∠MPE=60°,
∴PE=$\frac{1}{2}$PM=$\sqrt{3}$,同理可得CQ=2$\sqrt{3}$.FQ=$\sqrt{3}$,
∴EF=BC-PB-PE-FQ-QC=4$\sqrt{3}$,
∵ME=NF,ME∥NF,
∴四边形MEFN是平行四边形,
∴MN=EF=4$\sqrt{3}$.
(3)如图2中,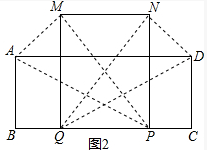
在Rt△ABP中,∵∠B=90°,AB=6,∠APB=30°,
∴PB=$\sqrt{3}$AB=6$\sqrt{3}$,
∴CQ=BP=6$\sqrt{3}$,
∵四边形MNPQ是矩形,
∴∠NPQ=90°,
在Rt△QNP中,∵∠NPQ=90°,QN=QC=6$\sqrt{3}$,∠NQP=60°,
∴QP=$\frac{1}{2}$QN=3$\sqrt{3}$,
∴BQ=PC=3$\sqrt{3}$,
∴AD=BC=BQ+PQ+PC=9$\sqrt{3}$.
点评 本题考查四边形综合题、翻折变换、全等三角形的判定和性质、矩形的性质,直角三角形30度角性质等知识,解题的关键是灵活应用这些知识解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在Rt△ABC中,∠ABC=90°,AB=BC,点D是线段AB上的一点,连接CD,过点B作BG⊥CD,分别交CD,CA于点E,F,与过点A且垂直于AB的直线相交于点G,连接DE给出以下四个结论:
如图,在Rt△ABC中,∠ABC=90°,AB=BC,点D是线段AB上的一点,连接CD,过点B作BG⊥CD,分别交CD,CA于点E,F,与过点A且垂直于AB的直线相交于点G,连接DE给出以下四个结论:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 现在的乐陵已经实现村村通公路,现有两个城镇A、B与两条公路ME,MF位置如图所示,其中ME是东西方向的公路.现电信部门需在C处修建一座信号发射塔,要求发射塔到两个城镇A、B的距离必须相等,到两条公路ME,MF的距离也必须相等,且在∠FME的内部.
现在的乐陵已经实现村村通公路,现有两个城镇A、B与两条公路ME,MF位置如图所示,其中ME是东西方向的公路.现电信部门需在C处修建一座信号发射塔,要求发射塔到两个城镇A、B的距离必须相等,到两条公路ME,MF的距离也必须相等,且在∠FME的内部.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在?ABCD中,AB=12,AD=8,∠ABC的平分线交CD于点F,交AD的延长线于点E,CG⊥BE,垂足为G,若EF=2,则线段CG的长为( )
如图,在?ABCD中,AB=12,AD=8,∠ABC的平分线交CD于点F,交AD的延长线于点E,CG⊥BE,垂足为G,若EF=2,则线段CG的长为( )| A. | $\frac{15}{2}$ | B. | 4$\sqrt{3}$ | C. | 2$\sqrt{15}$ | D. | $\sqrt{55}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com