
.如图,在平面直角坐标系xOy中,抛物线 与x轴交于A,B两点,其中B(6,0),与y轴交于点C(0,8),点P是x轴上方的抛物线上一动点(不与点C重合).
与x轴交于A,B两点,其中B(6,0),与y轴交于点C(0,8),点P是x轴上方的抛物线上一动点(不与点C重合).
(1)求抛物线的表达式;
(2)过点P作PD⊥x轴于点D,交直线BC于点E,点E关于直线PC的对称点为 ,若点
,若点 落在y轴上(不与点C重合),请判断以P,C,E,
落在y轴上(不与点C重合),请判断以P,C,E, 为顶点
为顶点 的四边形的形状, 并说明理由;
的四边形的形状, 并说明理由;
(3)在(2)的 条件
条件 下直接写出点P的坐标.
下直接写出点P的坐标.
 |
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
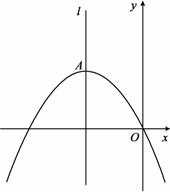 如图,顶点为A(-4,4)的二次函数图象经过原点(0,0),点P在该图象上,OP交其对称轴l于点M,点M、N关于点A对称,连接PN,ON.
如图,顶点为A(-4,4)的二次函数图象经过原点(0,0),点P在该图象上,OP交其对称轴l于点M,点M、N关于点A对称,连接PN,ON.
(1)求该二次函数的表达式;
(2)若点P的坐标是(-6,3),求△OPN的面积;
(3)当点P在对称轴l左侧的二次函数图象上运动时,
请解答下面问题:
① 求证:∠PNM=∠ONM;
② 若△OPN为直角三角形,请直接写出所有符合
条件的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
 随着生活质量的提高,人们的消费水平逐年上升,小明把自己家2010,2012,2014年的消费数据绘制统计图表如下:
随着生活质量的提高,人们的消费水平逐年上升,小明把自己家2010,2012,2014年的消费数据绘制统计图表如下:
年人均各项消费支出统计表
| 年份 支出项目(单位:元) | 2010年 | 2012年 | 2014年 |
| 食品支出 | a | 5 600 | 6 300 |
| 医疗、保健支出 | 2 000 | 2 200 | 3 000 |
| 家庭用品及服务支出 | 3 300 | 4 000 | 5 700 |
| 其他支出 | 2 500 | 4 200 | 6 000 |
根据以上信息解答下列问题:
(1)a= ;并补全条形统计图;
(2)我们把“食品支出总额占个人消费支出总额的百分数”叫做恩格尔系数,请分别求出小明家2010,2012,2014年的恩格尔系数,并根据变化情况谈谈你的看法.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山西农业大学附属中学八年级上学期期末考试数学试卷(解析版) 题型:解答题
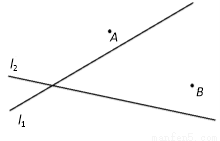
(8分)作图题有公路 同侧、
同侧、 异侧的两个城镇A、B,如下图,电信部门要修建一座信号发射塔,按照设计要求,发射塔到两个城镇A、B的距离必须相等,到两条公路
异侧的两个城镇A、B,如下图,电信部门要修建一座信号发射塔,按照设计要求,发射塔到两个城镇A、B的距离必须相等,到两条公路 、
、 的距离也必须相等,发射塔C应修建在什么位置?请用尺规作图找出所有符合条件的点,注明点C的位置。(保留作图痕迹,不写作法)。
的距离也必须相等,发射塔C应修建在什么位置?请用尺规作图找出所有符合条件的点,注明点C的位置。(保留作图痕迹,不写作法)。
查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省七年级上学期期末考试数学试卷(解析版) 题型:解答题
(本小题8分)如图,∠AOB=∠COD=90°,OC平分∠AOB,OE是∠BOD的三等分线.

(1)求∠BOD的度数;
(2)求∠COE的度数.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省八年级上学期期末考试数学试卷(解析版) 题型:选择题
图①,在边长为 的正方形中挖掉一个边长为
的正方形中挖掉一个边长为 的小正方形(
的小正方形( >
> ),把余下部分剪拼成一个矩形(如图②),通过计算两个图形的面积,验证了一个等式,则这个等式是( )
),把余下部分剪拼成一个矩形(如图②),通过计算两个图形的面积,验证了一个等式,则这个等式是( )

A、(a+2b)(a-b)= +ab-2
+ab-2
B、
C、
D、 -
- =(a+b)(a-b)
=(a+b)(a-b)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com