
【题目】如图,把一个含45°角的直角三角尺BEF和个正方形ABCD摆放在起,使三角尺的直角顶点和正方形的顶点B重合,连接DF,DE,M,N分别为DF,EF的中点,连接MA,MN,下列结论错误的是( )
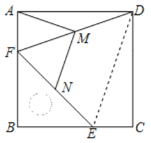
A. ∠ADF=∠CDEB. △DEF为等边三角形
C. AM=MND. AM⊥MN
【答案】B
【解析】
连接DE,先根据直角三角形的性质得出AM=![]() DF,再根据△BEF是等腰直角三角形得出AF=CE,由SAS定理得出△ADF≌△CDE,可得∠ADF=∠CDE ,DE=DF,再根据点M,N分别为DF,EF的中点,得出MN是△EFD的中位线,故MN=
DF,再根据△BEF是等腰直角三角形得出AF=CE,由SAS定理得出△ADF≌△CDE,可得∠ADF=∠CDE ,DE=DF,再根据点M,N分别为DF,EF的中点,得出MN是△EFD的中位线,故MN=![]() DE,MN∥DE,可得AM=MN,由MN∥DE,可得∠FMN=∠FDE,根据三角形外角性质可得∠AMF=2∠ADM,由∠ADM+∠DEC+∠FDE=∠FMN+∠AMF=90°,可得MA⊥MN,只能得到△DEF是等腰三角形,无法得出是等边三角形,据此即可得出结论.
DE,MN∥DE,可得AM=MN,由MN∥DE,可得∠FMN=∠FDE,根据三角形外角性质可得∠AMF=2∠ADM,由∠ADM+∠DEC+∠FDE=∠FMN+∠AMF=90°,可得MA⊥MN,只能得到△DEF是等腰三角形,无法得出是等边三角形,据此即可得出结论.
∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠BAD=∠C=90°,
∵点M是DF的中点,
∴AM=![]() DF,
DF,
∵△BEF是等腰直角三角形,
∴BF=BE,
∴AF=CE,
∴△ADF≌△CDE(SAS),
∴∠ADF=∠CDE ,DE=DF,
∵点M,N分别为DF,EF的中点,
∴MN是△EFD的中位线,
∴MN=![]() DE,
DE,
∴AM=MN;
∵MN是△EFD的中位线,
∴MN∥DE,
∴∠FMN=∠FDE,
∵AM=MD,
∴∠MAD=∠ADM,
∵∠AMF是△ADM外角,
∴∠AMF=2∠ADM.
又∵∠ADM=∠DEC,
∴∠ADM+∠DEC+∠FDE=∠FMN+∠AMF=90°,
∴MA⊥MN,
∵DE=DF,
∴△DEF是等腰三角形,无法得出是等边三角形,
综上,A、C、D正确,B错误,
故选B.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:
【题目】如图1,点M,N把线段AB分割成AM,MN和BN,若以AM,MN,BN为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点
(1)已知点M,N是线段AB的勾股分割点,若AM=3,MN=4,则BN的长为__________;
(2)已知点C是线段AB上的一定点,其位置如图2所示,请在BC上画一点D,使C,D是线段AB的勾股分割点(要求尺规作图,不写画法,保留作图痕迹,画出一种情形即可)
![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=AD,∠C=90°,以AB为直径的⊙O交AD于点E,CD=ED,连接BD交⊙O于点F.
(1)求证:BC与⊙O相切;
(2)若BD=10,AB=13,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB=AC,AB的垂直平分线MN交AC于点D,若∠A=36°,则下列结论:①∠C=72°;②BD是∠ABC的平分线;③△ADB是等腰三角形;④△BCD的周长=AB+BC.正确是______(填序号).
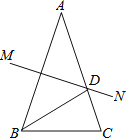
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若将边长为 a 、b 的正方形 ABCD 按图 ① 中的比例进行分割,可以拼成一个长方形A1 B1C1D1 不重叠、无缝隙),如图②所示.
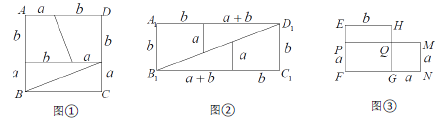
(1)根据图①可以拼成图②的面积关系,请写出 a 、b 之间存在的关系式;
(2)已知图③中,四边形 QMNG 与四边形EFGH 分别是以 a 、b 长为边的正方形与图①中的 a 、b 相同),在图 3 已有的四边形中,面积相等的四边形有几组?请分别写出.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,A(0,2),B(0,6),动点C在直线y=x上.若以A、B、C三点为顶点的三角形是等腰三角形,则点C的个数是( )
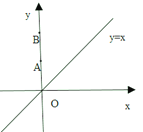
A. 6B. 5C. 4D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,A,B两点分别在x轴,y轴的正半轴上,且OA=OB,点C在第一象限,OC=3,连接BC,AC,若∠BCA=90°,则BC+AC的值为_________。
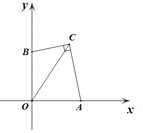
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() ,
,![]() ,若
,若![]() ,
,![]() ,
,
①四边形![]() 是平行四边形;
是平行四边形;
②![]() 是等腰三角形;
是等腰三角形;
③四边形![]() 的周长是
的周长是![]() ;
;
④四边形![]() 的面积是16.
的面积是16.
则以上结论正确的是![]()
![]()

A. ①②③B. ①②④C. ①③④D. ②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com