
| 1 |
| x1 |
| 1 |
| x2 |
| 4(n-1) |
| 4 |
| n2 |
| 4 |
| 1 |
| x1 |
| 1 |
| x2 |
| 4(1-n) |
| n2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 4(n-1) |
| 4 |
| n2 |
| 4 |
| 1 |
| x1 |
| 1 |
| x2 |
| x1+x2 |
| x1x2 |
| 1-n | ||
|
| 4(1-n) |
| n2 |
| 4(1-n) |
| n2 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| b |
| a |
| c |
| a |


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:初中数学 来源: 题型:
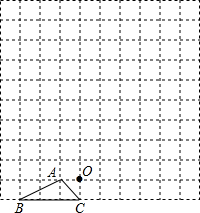 图中的小方格都是边长为1的正方形,△ABC的顶点和O点都在正方形的顶点上.以点O为位似中心,在方格图中将△ABC放大为原来的2倍,得到△A′B′C′,再将△A′B′C′绕点B′顺时针旋转90°,旋转后得到△A″B′C″,请将△A′B′C′和△A″B′C″在正方形中分别画出,并保留作图痕迹.
图中的小方格都是边长为1的正方形,△ABC的顶点和O点都在正方形的顶点上.以点O为位似中心,在方格图中将△ABC放大为原来的2倍,得到△A′B′C′,再将△A′B′C′绕点B′顺时针旋转90°,旋转后得到△A″B′C″,请将△A′B′C′和△A″B′C″在正方形中分别画出,并保留作图痕迹.查看答案和解析>>
科目:初中数学 来源: 题型:
| A型利润 | B型利润 | |
| 甲店 | 200 | 170 |
| 乙店 | 160 | 150 |
查看答案和解析>>
科目:初中数学 来源: 题型:
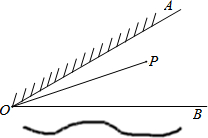 如图,∠AOB=30°,OA表示草地边,OB表示河边,点P表示家且在∠AOB内.某人要从家里出发先到草地边给马喂草,然后到河边喂水,最后回到家里.
如图,∠AOB=30°,OA表示草地边,OB表示河边,点P表示家且在∠AOB内.某人要从家里出发先到草地边给马喂草,然后到河边喂水,最后回到家里.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com