
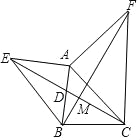
【题目】如图所示,已知AE⊥AB,AF⊥AC,AE=AB,AF=AC,AB与EC交于点D.问:
(1)EC与BF有什么大小关系?并说明理由.
(2)EC与BF的位置关系是__________.(直接写出结论,不证明)
【答案】(1)EC=BF;理由见解析;(2)EC⊥BF.
【解析】
(1)欲证明EC=BF,只要证明△AEC≌△ABF即可;
(2)依据AC交BF于D,利用“8字型”证明∠ABF+∠BDM=90°即可解决问题.
解:(1)EC=BF
理由:∵AE⊥AB,AF⊥AC,
∴∠BAE=∠CAF=90°,
∴∠BAE+∠BAC=∠CAF+∠BAC,即∠EAC=∠BAF,
在△ABF和△AEC中,
∵
∴△ABF≌△AEC(SAS),
∴EC=BF;
(2)根据(1),可得△ABF≌△AEC,
∴∠AEC=∠ABF,
∵AE⊥AB,
∴∠BAE=90°,
∴∠AEC+∠ADE=90°,
∵∠ADE=∠BDM(对顶角相等),
∴∠ABF+∠BDM=90°,
在△BDM中,∠BMD=180°﹣∠ABF﹣∠BDM=180°﹣90°=90°,
∴EC⊥BF.
故答案为:EC⊥BF.


科目:初中数学 来源: 题型:
【题目】如图是一组有规律的图案,它们是由边长相同的正方形和正三角形拼接而成,第①个图案有4个三角形和1个正方形,第②个图案有7个三角形和2个正方形,第③个图案有10个三角形和3个正方形,…依此规律,第n个图案有 ____________个三角形(用含n的代数式表示);

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD和正方形BEFG平放在一起.
(1)若两正方形的面积分别是16和9,直接写出边AE的长为 .
(2)①设正方形ABCD的边长为a,正方形BEFG的边长为b,求图中阴影部分的面积(用含a和b的代数式表示)
②在①的条件下,如果a+b=10,ab=16,求阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
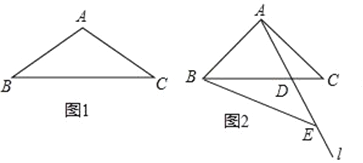
【题目】钝角三角形ABC中,∠BAC>90°,AB=AC,∠ACB=α,过点A的直线l交BC边于点D.点E在直线l上,且BC=BE.,点E在AD延长线上.
①当α=30°,点D恰好为BC中点时,补全图1直接写出∠BAE= °,
∠BEA= °;
②如图2,若∠BAE=2α,求∠BEA的度数(用含α的代数式表示);
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某班全体学生外出时选择乘车、步行、骑车人数的条形统计图和扇形统计图(两图都不完整),则下列结论中正确的是( )

A. 步行人数为30人 B. 骑车人数占总人数的10%
C. 该班总人数为50人 D. 乘车人数是骑车人数的40%
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个长方形运动场被分隔成![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 共
共![]() 个区,
个区, ![]() 区是边长为
区是边长为![]() 的正方形,
的正方形, ![]() 区是边长为
区是边长为![]() 的正方形.
的正方形.
(1)列式表示每个![]() 区长方形场地的周长,并将式子化简;
区长方形场地的周长,并将式子化简;
(2)列式表示整个长方形运动场的周长,并将式子化简;
(3)如果![]() ,
, ![]() ,求整个长方形运动场的面积.
,求整个长方形运动场的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知平移一次函数y=2x﹣4的图象过点(﹣2,1)后的图象为l1.
(1)求图象l1对应的函数表达式,并画出图象l1;
(2)求一次函数y=﹣2x+4的图象l2与l1及x轴所围成的三角形的面积.
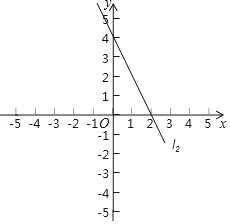
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一项工程,甲乙两人合作需要8天完成任务,若甲单独做需要12天完成任务.
(1)若甲乙两人一起做6天,剩下的由甲单独做,还需要几天完成?
(2)若甲乙两人一起做4天,剩下的由乙单独做,还需要几天完成?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com