【题目】已知平移一次函数y=2x﹣4的图象过点（﹣2，1）后的图象为l1．
（1）求图象l1对应的函数表达式，并画出图象l1；
（2）求一次函数y=﹣2x+4的图象l2与l1及x轴所围成的三角形的面积．
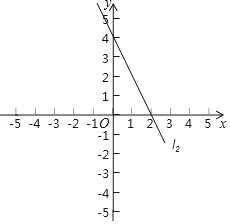
【答案】（1）l1对应的函数表达式为y=2x+5，画图见解析；（2）l2与l1及x轴所围成的三角形的面积为
．
【解析】
（1）根据平行一次函数的定义可知：k=2，再利用待定系数法求出b的值即可；
（2）过点A作AD⊥x轴于D点，利用三角形面积公式解答即可．
（1）由已知可设l1对应的函数表达式为y=2x+b，
把x=﹣2，y=1代入表达式解得：b=5，
∴l1对应的函数表达式为y=2x+5，
画图如下：
，
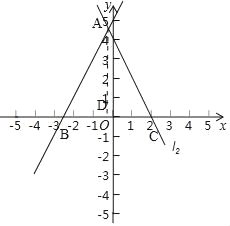（2）设l1与l2的交点为A，过点A作AD⊥x轴于D点，
由题意得
，解得
即A（
，
），则AD=，
设l1、l2分别交x轴的于点B、C，
由y=﹣2x+4=0，解x=2，即C（2，0）
由y=2x+5=0解得
，即B（
，0）
∴BC=，
∴
即l2与l1及x轴所围成的三角形的面积为
．
科目：初中数学 来源： 题型：
【题目】对于实数a，我们规定：用符号[
]表示不大于
的最大整数，称[
]为a的根整数，例如：[
]=3，[
]=3．
（1）仿照以上方法计算：[
] = ；[
] = ．
（2）若[
]=1，写出满足题意的x的整数值 ．
如果我们对a连续求根整数，直到结果为1为止．例如：对10连续求根整数2次 [
]=3→[
]=1，这时候结果为1．
（3）对100连续求根整数， 次之后结果为1．
（4）只需进行3次连续求根整数运算后结果为1的所有正整数中，最大的是 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
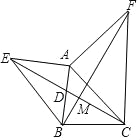
【题目】如图所示，已知AE⊥AB，AF⊥AC，AE=AB，AF=AC，AB与EC交于点D．问：
（1）EC与BF有什么大小关系？并说明理由.
（2）EC与BF的位置关系是__________.（直接写出结论，不证明）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，小红晚上在一条笔直的小路上由A处径直走到B处，小路的正中间有一盏路灯，那么小红在灯光照射下的影长l与她行走的路程s之间的变化关系用图象刻画出来大致是（ ）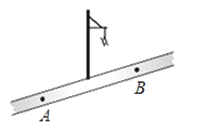
A.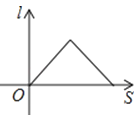
B.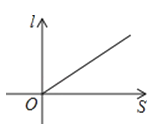
C.
D.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知多项式2x2+
x3+x﹣5x4﹣
．
(1)请指出该多项式是几次几项式，并写出它的二次项、一次项和常数项；
(2)按要求把这个多项式重新排列：①按x的降幂排列；②按x的升幂排列．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC沿直线l向右移了3厘米，得△FDE，且BC＝6厘米，∠B＝40°.
(1)求BE；
(2)求∠FDB的度数；
(3)找出图中相等的线段(不另添加线段)；
(4)找出图中互相平行的线段(不另添加线段)．
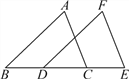
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在三角形ABC中，BC=14，AC=9，AB=13，它的内切圆分别和BC、AC、AB切于点D、E、F，那么AF、BD、CE的长分别为（ ）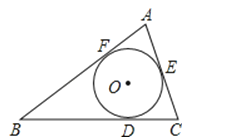
A.AF=4，BD=9，CE=5
B.AF=4，BD=5，CE=9
C.AF=5，BD=4，CE=9
D.AF=9，BD=4，CE=5
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，Rt△ABC的内切圆⊙O与AB、BC、CA分别相切于点D、E、F，且∠ACB=90°，AB=5，BC=3，点P是边AC上的一动点，PH⊥AB，垂足为H．
（1）求⊙O的半径的长及线段AD的长；
（2）设PH=x，PC=y，求y关于x的函数关系式．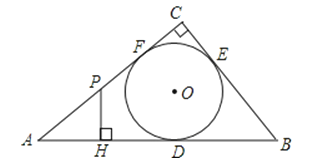
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】计算：
(1)(－10xy3)·2xy4z；
(2)(－4x)(2x2－2x－1);
(3)0.4x2y·
－(－2x)3·xy3；
(4)－3a
＋2b(a2－ab)－2a2(b＋3)．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com