练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】抛物线y=（x﹣1）2+3的对称轴是（ ）
    A.直线x=1
    B.直线x=3
    C.直线x=﹣1
    D.直线x=﹣3

    【答案】A
    【解析】解：抛物线y=（x﹣1）2+3的对称轴是直线x=1．
    故选A．
    【考点精析】掌握二次函数的性质是解答本题的根本，需要知道增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】若一个多边形的每一个外角都等于40°，则这个多边形的边数是（ ）
    A.7
    B.8
    C.9
    D.10

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列轴对称图形中，对称轴条数最少的是（ ）
    A.等边三角形
    B.正方形
    C.正六边形
    D.圆

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下面方格中有一个菱形ABCD和点O，请你在方格中画出以下图形（只要求画出平移、旋转后的图形，不要求写出作图步骤和过程）．

    （1）画出菱形ABCD向右平移6格后的四边形A1B1C1D1；

    （2）画出菱形ABCD以点O为旋转中心，沿逆时针方向旋转90°后的四边形A2B2C2D2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】学校举行百科知识抢答赛，共有20道题，规定每答对一题记10分，答错或放弃记﹣4分，八年级一班代表的得分目标为不低于88分，则这个队至少要答对道题才能达到目标要求．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】【问题情境】一节数学课后，老师布置了一道课后练习题：

    如图：已知在Rt△ABC中，AC=BC，∠ACB=90°，CD⊥AB于点D，点E、F分别在A和BC上，∠1=∠2，FG⊥AB于点G，求证：△CDE≌△EGF．

    （1）阅读理解，完成解答

    本题证明的思路可用下列框图表示：

    根据上述思路，请你完整地书写这道练习题的证明过程；

    （2）特殊位置，证明结论

    若CE平分∠ACD，其余条件不变，求证：AE=BF；

    （3）知识迁移，探究发现

    如图，已知在Rt△ABC中，AC=BC，∠ACB=90°，CD⊥AB于点D，若点E是DB的中点，点F在直线CB上且满足EC=EF，请直接写出AE与BF的数量关系．（不必写解答过程）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

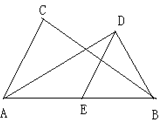
    【题目】在△ABC中,AD平分∠BAC，BD⊥AD于D，过D作DE∥AC交AB于点E.

    （1）求证：E是AB的中点；

    （2）若AB＝6，求线段DE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】抛物线y=﹣x2+3的顶点坐标是（　　）

    A. （0，3） B. （1，3） C. （﹣1，﹣3） D. （2，﹣3）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】课题学习

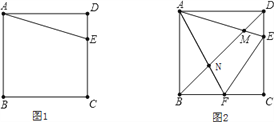
    问题背景1 甲、乙、丙三名同学探索课本上一道题：如图1，E是边长为a的正方形ABCD中CD边上任意一点，以点A为中心，把△ADE顺时针旋转90°，

    （1）①在图1中画出旋转后的图形；②图1中，与线段AE垂直的线段是 ，说明你的理由；

    问题背景2 在正方形ABCD中，∠EAF=45°，点F为BC上一点，点E为DC上一点，∠EAF的两边AE、AF分别与直线BD交于点M、N．连接EF。继续探索时，

    甲发现：线段BF，EF，DE之间存在着关系式EF=BF+DE；

    乙发现：△CEF的周长是一个恒定不变的值；

    丙发现：线段BN，MN，DM之间存在着关系式BN2+DM2=MN2

    （2）请你对甲、乙、两三人中一个结论进行研究，作出判断，并说明你的理由。

    查看答案和解析>>

    同步练习册答案