
����Ŀ������ѧϰ
���ⱳ��1 �ס��ҡ�������ͬѧ̽���α���һ���⣺��ͼ1��E�DZ߳�Ϊa��������ABCD��CD��������һ�㣬�Ե�AΪ���ģ��ѡ�ADE˳ʱ����ת90�㣬
��1������ͼ1�л�����ת���ͼ�Σ���ͼ1�У����߶�AE��ֱ���߶��� ��˵��������ɣ�
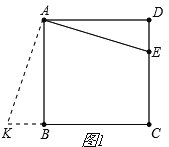
���ⱳ��2 ��������ABCD�У���EAF=45�㣬��FΪBC��һ�㣬��EΪDC��һ�㣬��EAF������AE��AF�ֱ���ֱ��BD���ڵ�M��N������EF������̽��ʱ��
���֣��߶�BF��EF��DE֮������Ź�ϵʽEF=BF+DE��
�ҷ��֣���CEF���ܳ���һ���㶨�����ֵ��
�����֣��߶�BN��MN��DM֮������Ź�ϵʽBN2+DM2=MN2
��2������Լס��ҡ���������һ�����۽����о��������жϣ���˵��������ɡ�
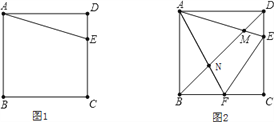
���𰸡�(1) ����ͼ������;��AK��AE,���ɼ�����;(2) �ס��ҡ�������ͬѧ�ķ��ֶ�����ȷ��.���ɼ�����.
���������������: ��1������ͼ����תǰ�������ɵ���ͼ��ȫ�Ȼ���ͼ�μ��ɣ�
��2����ѡ��ף��ӳ�CB��K��ʹBK=DE����AK����ͼ����ת�����ʿɵ���AKB�ա�AED���ɵó���KAF=��FAE�������ɵó���AKF�ա�AEF����ȫ�������ε����ʼ�BK=DE�ɵó�EF=BF+DE��
��ѡ���ң��ӳ�CB��K��ʹBK=DE����AK����ͼ����ת�����ʿɵ���AKB�ա�AED����ȫ�������ε����ʿɵõ���AKF�ա�AEF���ٸ���BK=DE���ɵó���CEF�ܳ�Ϊ��ֵ��
��ѡ�������AK�Ͻ�ȡAG=AM������BG��GN����ͼ����ת�����ʿɵ���ABG�ա�ADM����GAN�ա�NAM�����ɹ��ɶ������ɵó�BN2+DM2=MN2��
�������:
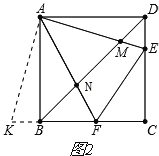
��ͼ��ͼ1��
�ӳ�CB��K��ʹBK=DE��
���ı���ABCD�������Σ�
��AD=AB,��ADE=��ABK=��BAD=90��
���ADE�ա�ABK��
���DAE=��BAK��
���EAK=��BAK+��BAE=��DAK+��BAE=��BAD=90��
��AK��AE.
�ʴ�ΪAK��AE.
(2)ѡ����֣�
֤������ͼ2��
�ӳ�CB��K,ʹBK=DE,��AK,����AKB�ա�AED��
�ߡ�BAF+��DAE=45����
���KAF=45����
���KAF=��FAE.
��AK=AE��AF=AF��
���AKF�ա�AEF.
��KF=EF.
�֡�BK=DE��
��EF=BF+DE
ѡ���ҷ��֣�
֤������ͼ2��

�ӳ�CB��K,ʹBK=DE,��AK,���AKB�ա�AED
�ߡ�BAF+��DAE=45����
���KAF=45����
���KAF=��FAE.
��AK=AE��AF=AF��
���AKF�ա�AEF.
��KF=EF.
�֡�BK=DE��
��EF=BF+DE
��CEF�ܳ�=CF+CE+EF=CF+CE+(BF+DE)=(CF+BF)+(CE+DE)=BC+DC=2a(��ֵ)
ѡ������֣�
֤������ͼ3��
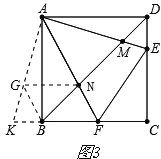
��AK�Ͻ�ȡAG=AM������BG��GN.
��AG=AM��AB=AD����KAB=��EAD��
���ABG�ա�ADM��
��BG=DM,��ABG=��ADB=45��.
�֡ߡ�ABD=45����
���GBD=90��.
�ߡ�BAF+��DAE=45����
���KAF=45����
���KAF=��FAE.
�֡�AG=AM��AN=AN��
���GAN�ա�NAM.
��NG=MN��
�ߡ�GBD=90����
��BG +BN =NG ��
��BN +DM =MN .
�����������ס��ҡ�������ͬѧ�ķ��ֶ�����ȷ�ġ�
�㾦:���⿼�����ͼ�ε���ת,ͨ����ת,����ȫ��������,���ֱߵĹ�ϵ,������ֱ�������εĹ��ɶ����ҵ������߶ε�ƽ����ϵ,���ù��취֤����AKF�ա�AEF, ��GAN�ա�NAM�ǽ�����Ĺؼ�.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������y=��x��1��2+3�ĶԳ����ǣ� ��
A.ֱ��x=1
B.ֱ��x=3
C.ֱ��x=��1
D.ֱ��x=��3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У���O�ڶԽ���AC�ϣ���OA�ij�Ϊ�뾶��ԲO��AD��AC�ֱ��ڵ�E��F���ҡ�ACB=��DCE��
��1���ж�ֱ��CE���O��λ�ù�ϵ����֤����Ľ��ۣ�
��2����tan��ACB=![]() ��BC=2�����O�İ뾶��
��BC=2�����O�İ뾶��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����и�ʽ�����ҵı��Σ�����ʽ�ֽ���ǣ� ��
A.x2��9+6x=��x+3����x��3��+6x
B.��x+5����x��2��=x2+3x��10
C.x2��8x+16=��x��4��2
D.6ab=2a3b
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ʒ�ijɱ����꽵����75%��ƽ��ÿ��ݽ���������
A. 50% B. 25% C. 37.5% D. ���ϴ𰸶�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�����ѵ���У��ס������˸���� 10 �Σ����� 10 ������ɼ���ƽ�������� 8.9 ��������ֱ��� S ��2��1.7��S �� 2=1.2������ڼס���������������ѵ���гɼ��ȶ���___________��(����������������)
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com