
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 一次函数当a>0时,函数值y总是随自变量x增大而增大,反比例函数当k<0时,在每一个象限内,y随自变量x增大而增大,二次函数根据对称轴及开口方向判断增减性.
解答 解:①为一次函数,且a>0时,函数值y总是随自变量x增大而增大;
②为一次函数,且a<0时,函数值y总是随自变量x增大而减小;
③为反比例函数,当x>0或者x<0时,函数值y随自变量x增大而增大,当-2<x<2时,就不能确定增减性了;
④为二次函数,对称轴为x=-3,开口向上,故当-2<x<2时,函数值y随自变量x增大而增大,
符合题意的是①④,
故选B.
点评 本题考查了一次函数、反比例函数、二次函数的增减性;熟练掌握一次函数、二次函数、反比例函数的性质是关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
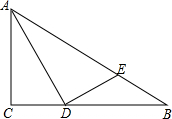 已知,如图,在Rt△ABC中,∠ACB=90°,AB=4,AD是∠BAC的平分线,过点D作DE⊥AD,垂足为点D,交AB于点E,且$\frac{BE}{AB}=\frac{1}{4}$.
已知,如图,在Rt△ABC中,∠ACB=90°,AB=4,AD是∠BAC的平分线,过点D作DE⊥AD,垂足为点D,交AB于点E,且$\frac{BE}{AB}=\frac{1}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
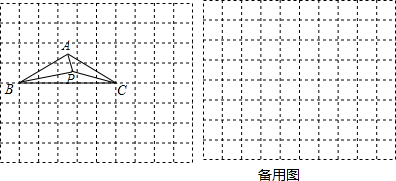
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

| 运动员 | 平均数 | 众数 | 中位数 | 方差 |
| 甲 | 601.8 | 600 | 600 | 50.56 |
| 乙 | 599.3 | 618 | 595.5 | 284.21 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
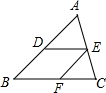 如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,若DE∥BC,EF∥AB,则下面所列比例式中正确的是( )
如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,若DE∥BC,EF∥AB,则下面所列比例式中正确的是( )| A. | $\frac{AD}{BD}$=$\frac{DE}{BC}$ | B. | $\frac{BF}{BC}$=$\frac{EF}{AD}$ | C. | $\frac{AE}{EC}$=$\frac{BF}{CF}$ | D. | $\frac{EF}{AB}$=$\frac{DE}{BC}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com