
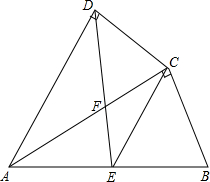
 如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点.
如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点.分析 (1)根据相似三角形的判定与性质,可得$\frac{AD}{AC}$=$\frac{AC}{AB}$,根据比例的性质,可得答案;
(2)根据直角三角形的性质,可得CE与AE的关系,根据等腰三角形的性质,可得∠EAC=∠ECA,根据角平分线的定义,可得∠CAD=∠CAB,根据平行线的判定,可得答案.
解答 证明:(1)∵AC平分∠BAD,
∴∠DAC=∠CAB.
∵∠ADC=∠ACB=90°,
∴△ADC∽△ACB,
∴$\frac{AD}{AC}$=$\frac{AC}{AB}$,
AC2=AB•AD;
(2)∵E是AB的中点,
∴CE=$\frac{1}{2}$AB=AE,
∴∠EAC=∠ECA.
∵AC平分∠DAB,
∴∠CAD=∠CAB,
∴∠CAD=∠ECA,
∴CE∥AD.
点评 本题考查了相似三角形的判定与性质,(1)利用了相似三角形的判定与性质,比例的性质;(2)利用了直角三角形的性质,等腰三角形的性质,平行线的判定.


科目:初中数学 来源: 题型:填空题
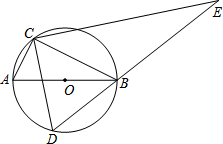 如图,AB是⊙O的直径,点C在⊙O上,D是⊙O上的一个动点,且C,D两点位于直径AB的两侧.连接CD,过点C作CE⊥CD交DB的延长线于点E.若AC=2,BC=4,则线段DE长的最大值是10.
如图,AB是⊙O的直径,点C在⊙O上,D是⊙O上的一个动点,且C,D两点位于直径AB的两侧.连接CD,过点C作CE⊥CD交DB的延长线于点E.若AC=2,BC=4,则线段DE长的最大值是10.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
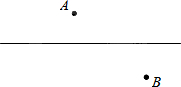 如图,在公路l的两旁有两个工厂A、B,要在公路上搭建一个货场让A、B两厂使用,要使货场到A、B两厂的距离之和最小,问货场应建在什么位置?为什么?
如图,在公路l的两旁有两个工厂A、B,要在公路上搭建一个货场让A、B两厂使用,要使货场到A、B两厂的距离之和最小,问货场应建在什么位置?为什么?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
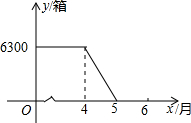 某工厂生产空气清新剂,今年4月份后,每天的产量与销售量均为500箱,进入4月份后,每天的产量保持不变,市场需求量不断增加.如图是四月前后一段时期库存量y(箱)与生产时间t(月份)之间的函数图象.
某工厂生产空气清新剂,今年4月份后,每天的产量与销售量均为500箱,进入4月份后,每天的产量保持不变,市场需求量不断增加.如图是四月前后一段时期库存量y(箱)与生产时间t(月份)之间的函数图象.| 型号 | A | B |
| 价格(万元/台) | 28 | 25 |
| 日产量(箱/台) | 50 | 40 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 按要求在图中画图,并把答案填写在横线上.
按要求在图中画图,并把答案填写在横线上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
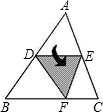 如图,D、E为△ABC两边AB、AC上的两点,将△ABC沿线段DE折叠,使得DE∥BC,且点A落在点F处,若∠B=55°,则∠BDF为( )
如图,D、E为△ABC两边AB、AC上的两点,将△ABC沿线段DE折叠,使得DE∥BC,且点A落在点F处,若∠B=55°,则∠BDF为( )| A. | 55° | B. | 60° | C. | 70° | D. | 不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 尺码(厘米) | 100 | 105 | 110 | 115 | 120 | 125 | 130 |
| 销售量(件) | 1 | 2 | 5 | 11 | 7 | 3 | 1 |
| A. | 105 | B. | 110 | C. | 115 | D. | 120 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com