Question

如图，求梯形DBCE的面积．

Answer 1

考点：面积及等积变换

专题：

分析：首先设S_△DOE=a，BE与CD交于O，由DE∥BC，可得△ADE∽△ABC，△DOE∽△COB，即可证得AD：AB=OE：OB，然后根据等高三角形的面积比等于对应底的比，可证得S_△ADE：S_△ABE=S_△DOE：S_△BOD，则可得方程：

20

20+6+a

=

a

6

，解此方程即可求得△DOE的面积，然后由相似三角形面积比等于相似比的平方，求得△COB的面积，继而求得答案．

解答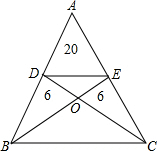：解：设S_△DOE=a，BE与CD交于O，
∵DE∥BC，
∴△ADE∽△ABC，△DOE∽△COB，
∴AD：AB=DE：BC，OE：OB=DE：BC，
∴AD：AB=OE：OB，
∵S_△ADE：S_△ABE=AD：AB，S_△DOE：S_△BOD=OE：OB，
∴S_△ADE：S_△ABE=S_△DOE：S_△BOD，
∴

20

20+6+a

=

a

6

，
∴a²+26a-120=0，
即（a+30）（a-4）=0，
解得：a=4或a=-30（舍去），
∴S_△DOE=4，
∴DE：BC=OE：OB=4：6=2：3，
∵

S△DOE

S△COB

=(

DE

BC

)2=

4

9

，
∴S_△COB=9，
∴S_梯形DBCE=S_△DOE+S_△BOD+S_△COE+S_△COB=4+6+6+9=25．

点评：此题考查了面积与等积变换，涉及了相似三角形的判定与性质以及梯形的性质．此题难度较大，注意掌握数形结合思想与方程思想的应用．