
【题目】在平面直角坐标系中,点A![]() 点B
点B![]() 已知
已知![]() 满足
满足![]() .
.
(1)点A的坐标为_________,点B的坐标为__________;
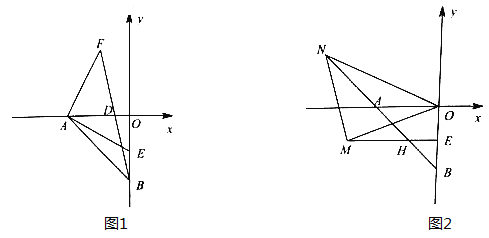
(2)如图1,点E为线段OB上一点,连接AE,过A作AF⊥AE,且AF=AE,连接BF交![]() 轴于点D,若点D(-1,0),求点E的坐标;
轴于点D,若点D(-1,0),求点E的坐标;
(3)在(2)的条件下,如图2,过E作EH⊥OB交AB于H,点M是射线EH上一点(点M不在线段EH上),连接MO,作∠MON=45°,ON交线段BA的延长线于点N,连接MN,探究线段MN与OM的关系,并说明理由。
【答案】(1)(-4,0) (0,-4)
(2)E(0,-2)
(3)MN⊥OM,MN=OM
【解析】
(1)先将式子变形为完全平方公式的形式,再根据平方的非负性求解;
(2)如图1中,作FH⊥OA于H,由△AFH≌△EAO,推出FH=OA,由△FDH≌△BDO,推出AH=OH=OE=2;
(3)连接OH,OM与BN交于G,由△NGO∽△MGH,推出![]() =
=![]() ,再推出
,再推出![]() =
=![]() ,再得出△NGM∽△OGH,推出∠NMG=∠OHG=90°,推出△OMN是等腰直角三角形即可解决问题.
,再得出△NGM∽△OGH,推出∠NMG=∠OHG=90°,推出△OMN是等腰直角三角形即可解决问题.
(1)∵![]() =0,
=0,
∴a=-4,b=-4,
∴点A的坐标为(-4,0),点B的坐标为(0,-4)
(2)作FH⊥OA于H,
∵AF⊥AE,
∴∠FAE=∠AHF=∠AOE=90°,
∴∠FAH+∠OAE=90°,∠FAH+∠AFH=90°,
∴∠AFH=∠OAE,
∵AF=OA,
∴△AFH≌△EAO,
∴FH=OA,
∵点A(-4,0),点B(0,-4)
∴FH=OA=OB=4,
∵∠FHD=∠BOD=90°,∠FDH=∠BDO,
∴△FDH≌△BDO,
∴OD=DH=1,
∴AH=OH=OE=2,
∴E(0,-2)
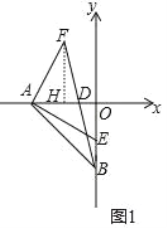
(3)结论:MN=OM,MN⊥OM,
理由:连接OH,OM与BN交于G,
∵OA=OB,∠AOB=45°,
∴∠OAB=45°
∵OE=EB=2,EH∥OA,
∴AH=BH,OH⊥AB,∠AHM=∠OAB=45°,
∵∠MON=45°
∴∠GON=∠GHM,
∵∠NGO=∠MGH,
∴△NGO∽△MGH,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∵∠NGM=∠OGH,
∴△NGM∽△OGH,
∴∠NMG=∠OHG=90°,
∴△OMN是等腰直角三角形
∴MN=OM,MN⊥OM.


科目:初中数学 来源: 题型:
【题目】如图,已知MB=ND,∠MBA=∠NDC,下列条件中不能判定△ABM≌△CDN的是( )

A. ∠M=∠N B. AM=CN C. AB=CD D. AM∥CN
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O中,直径CD⊥弦AB于E,AM⊥BC于M,交CD于N,连AD.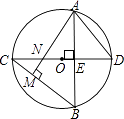
(1)求证:AD=AN;
(2)若AB=4 ![]() ,ON=1,求⊙O的半径.
,ON=1,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
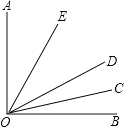
【题目】如图,已知∠AOB内部有三条射线,OE平分∠AOD,OC平分∠BOD.
(1)若∠AOB=90°,求∠EOC的度数;
(2)若∠AOB=α,求∠EOC的度数;
(3)如果将题中“平分”的条件改为∠EOA=![]() ∠AOD,∠DOC=
∠AOD,∠DOC=![]() ∠DOB且∠DOE:∠DOC=4:3,∠AOB=90°,求∠EOC的度数.
∠DOB且∠DOE:∠DOC=4:3,∠AOB=90°,求∠EOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°,求∠APC的度数.
小明的思路是:过P作PE∥AB,通过平行线性质来求∠APC.
(1)按小明的思路,易求得∠APC的度数为_____度;
(2)问题迁移:如图2,AB∥CD,点P在射线OM上运动,记∠PAB=α,∠PCD=β,当点P在B、D两点之间运动时,问∠APC与α、β之间有何数量关系?请说明理由;
(3)在(2)的条件下,如果点P在B、D两点外侧运动时(点P与点O、B、D三点不重合),请直接写出∠APC与α、β之间的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,矩形ABCD的边AD=3,A(![]() ,0),B(2,0),直线y=kx+b经过B,D两点.
,0),B(2,0),直线y=kx+b经过B,D两点.
(1)求直线y=kx+b的解析式;
(2)将直线y=kx+b平移,若它与矩形有公共点,直接写出b的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,以BC为直径的⊙O交AB于点D,E是AC的中点,OE交CD于点F.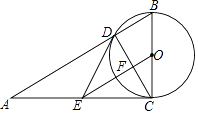
(1)若∠BCD=36°,BC=10,求BD的长;
(2)判断直线DE与⊙O的位置关系,并说明理由;
(3)求证:2CE2=ABEF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了增强学生体质,决定开设以下体育课外活动项目:A篮球、B乒乓球、C跳绳、D踢毽子,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:
(1)这次被调查的学生共有人;
(2)请你将条形统计图补充完成;
(3)在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com