
【题目】如图,△ABC是等腰直角三角形,∠ACB=90°,D是射线CB上一点(点D不与点B重合),以AD为斜边作等腰直角三角形ADE(点E和点C在AB的同侧),连接CE.

(1)如图①,当点D与点C重合时,直接写出CE与AB的位置关系;
(2)如图②,当点D与点C不重合时,(1)的结论是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由;
(3)当∠EAC=15°时,请直接写出![]() 的值.
的值.
【答案】(1)当点D与点C重合时,CE∥AB,理由见解析;(2)当点D与点C不重合时,(1)的结论仍然成立,理由见解析;(3)当∠EAC=15°时,![]() 的值为
的值为![]() 或
或![]() .
.
【解析】
(1)根据等腰直角三角形的性质、平行线的判定定理解答;
(2)在AF上截取AF=CD,连接EF,证明△EAF≌△EDC,根据全等三角形的性质得到EF=EC,∠AEF=∠DEC,根据平行线的判定定理证明;
(3)分图②、图③两种情况,根据全等三角形的性质、等腰直角三角形的性质计算,得到答案.
(1)当点D与点C重合时,CE∥AB,
理由如下:∵△ABC是等腰直角三角形,
∴∠CAB=45°,
∵△ADE是等腰直角三角形,
∴∠ADE=45°,
∴∠CAB=∠ADE,
∴CE∥AB;
(2)当点D与点C不重合时,(1)的结论仍然成立,
理由如下:在AC上截取AF=CD,连接EF,
∵∠AED=∠ACB=90°,
∴∠EAF=∠EDC,
在△EAF和△EDC中,
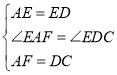 ,
,
∴△EAF≌△EDC(SAS),
∴EF=EC,∠AEF=∠DEC,
∵∠AED=90°,
∴∠FEC=90°,
∴∠ECA=45°,
∴∠ECA=∠CAB,
∴CE∥AB;
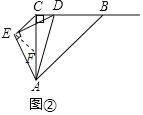
(3)如图②,∠EAC=15°,
∴∠CAD=30°,
∴AD=2CD,![]() ,
,
∴![]() ,
,
∵△CEF为等腰直角三角形,
∴![]() ,
,
∵△ABC是等腰直角三角形,
∴![]() ,
,
∴ ,
,
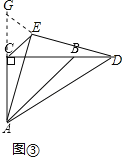
如图③,∠EAC=15°,
由(2)得,∠EDC=∠EAC=15°,
∴∠ADC=30°,
∴![]() ,
,
延长AC至G,使AG=CD,
∴CG=AG﹣AC=DC﹣AC=![]() AC﹣AC,
AC﹣AC,
在△EAG和△EDC中,
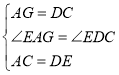 ,
,
∴△EAG≌△EDC(SAS),
∴EG=EC,∠AEG=∠DEC,
∴∠CEG=90°,
∴△CEG为等腰直角三角形,
∴![]() ,
,
∴![]() ,
,
综上所述,当∠EAC=15°时,![]() 的值为
的值为![]() 或
或![]() .
.


 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:
【题目】如图1,在四边形ABCD中,点E、F分别是AB、CD的中点,过点E作AB的垂线,过点F作CD的垂线,两垂线交于点G,连接GA、GB、GC、GD、EF,若∠AGD=∠BGC.
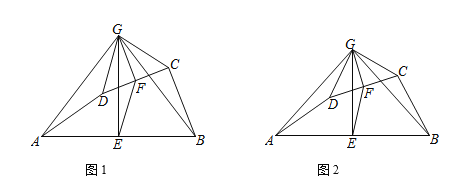
(1)求证:AD=BC;
(2)求证:△AGD∽△EGF;
(3)如图2,若AD、BC所在直线互相垂直,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周长相等的正三角形、正四边形、正六边形的面积S3、S4、S6间的大小关系是( )
A. S3>S4>S6 B. S6>S4>S3 C. S6>S3>S4 D. S4>S6>S3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:抛物线y=(m-1)x2+mx+m2-4的图象经过原点,且开口向上.
(1)确定![]() 的值;
的值;
(2)求此抛物线的顶点坐标;
(3)画出抛物线的图象,结合图象回答:当![]() 取什么值时,
取什么值时,![]() 随
随![]() 的增大而增大?
的增大而增大?
(4)结合图象直接回答:当![]() 取什么值时,
取什么值时,![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了解学生“第二课堂“活动的选修情况,对报名参加A.跆拳道,B.声乐,C.足球,D.古典舞这四项选修活动的学生(每人必选且只能选修一项)进行抽样调查.并根据收集的数据绘制了图①和图②两幅不完整的统计图.
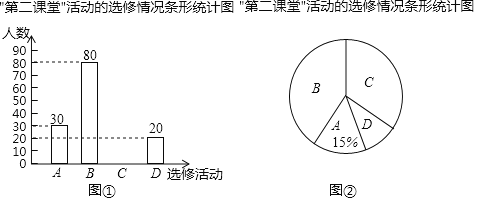
根据图中提供的信息,解答下列问题:
(1)本次调查的学生共有 人;在扇形统计图中,B所对应的扇形的圆心角的度数是 ;
(2)将条形统计图补充完整;
(3)在被调查选修古典舞的学生中有4名团员,其中有1名男生和3名女生,学校想从这4人中任选2人进行古典舞表演.请用列表或画树状图的方法求被选中的2人恰好是1男1女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙三个盒子中分别装有除颜色外都相同的小球,甲盒中装有两个球,分别为一个红球和一个绿球;乙盒中装有三个球,分别为两个绿球和一个红球;丙盒中装有两个球,分别为一个红球和一个绿球,从三个盒子中各随机取出一个小球
(1)请画树状图,列举所有可能出现的结果
(2)请直接写出事件“取出至少一个红球”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
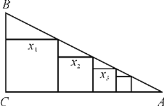
【题目】如图所示,在Rt△ABC中,∠C=90°,BC=1,AC=4,把边长分别为![]() ,
,![]() ,
,![]() ,…,
,…,![]() 的n
的n![]() 个正方形依次放入△ABC中,则第n个正方形的边长
个正方形依次放入△ABC中,则第n个正方形的边长![]() _______________(用含n的式子表示).
_______________(用含n的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,完成相应学习任务
旋转对称
把正n边形绕着它的中心旋转![]() 的整数倍后所得的正n边形重合.我们说,正n边形关于其中心有
的整数倍后所得的正n边形重合.我们说,正n边形关于其中心有![]() 的旋转对称.一般地,如果一个图形绕着某点O旋转角α(0<α<360°)后所得到的图形与原图形重合,则称此图形关于点O有角α的旋转对称.图1就是具有旋转对称性质的一些图形.
的旋转对称.一般地,如果一个图形绕着某点O旋转角α(0<α<360°)后所得到的图形与原图形重合,则称此图形关于点O有角α的旋转对称.图1就是具有旋转对称性质的一些图形.

任务:
(1)如图2,正六边形关于其中心O有 的旋转对称,中心对称图形关于其对称中心有 的旋转对称;
(2)图3是利用旋转变换设计的具有旋转对称性的一个图形,将该图形绕其中心至少旋转 与原图形重合;
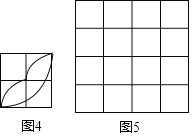
(3)请以图4为基本图案,在图5中利用平移、轴对称或旋转进行图案设计,使得设计出的图案是中心对称图形.
查看答案和解析>>
科目:初中数学 来源: 题型:
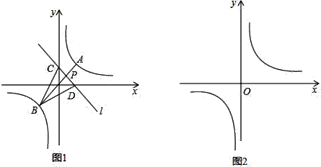
【题目】如图,点![]() 在反比例函数
在反比例函数![]() 第一象限的图象上,连接
第一象限的图象上,连接![]() ,延长
,延长![]() 与双曲线的另一支交于点
与双曲线的另一支交于点![]() ,作
,作![]() 的垂直平分线
的垂直平分线![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() .
.
(1)在图![]() 中,当
中,当![]() ,直接写出
,直接写出![]() ,
,![]() ,
,![]() 三点的坐标,并求出直线
三点的坐标,并求出直线![]() 的解析式.
的解析式.
(2)当点![]() 的坐标为
的坐标为![]() 时,利用图
时,利用图![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com