
【题目】菲尔兹奖是国际上有崇高声誉的一个数学奖项,下面的数据是从1936年至2014年菲尔兹奖得主获奖时的年龄(岁): 29 39 35 33 39 27 33 35 31 31 37 32 38 36
31 39 32 38 37 34 29 34 38 32 35 36 33 32
29 35 36 37 39 38 40 38 37 39 38 34 33 40
36 36 37 40 31 38 38 40 40 37 35 40 39 37
请根据上述数据,解答下列问题:
小彬按“组距为5”列出了如图的频数分布表
分组 | 频数 |
A:25~30 | |
B:30~35 | 15 |
C:35~40 | 31 |
D:40~45 | |
合计 | 56 |
(1)每组数据含最小值不含最大值,请将表中空缺的部分补充完整,并补全频数分布直方图; 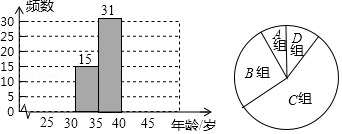
(2)根据(1)中的频数分布直方图描述这56位菲尔兹奖得主获奖时的年龄的分布特征;
(3)在(1)的基础上,小彬又画了如图所示的扇形统计图,图中获奖年龄在30~35岁的人数约占获奖总人数的%(百分号前保留1位小数);C组所在扇形对应的圆心角度数约为°(保留整数)
【答案】
(1)解:4|6
补全频数分布直方图如下:

(2)解:由频数分布直方图知,这56位菲尔兹奖得主获奖时的年龄主要分布在35~40岁
(3)26.8;199
【解析】解:(1)补全频数分布表如下:
分组 | 频数 |
A:25~30 | 4 |
B:30~35 | 15 |
C:35~40 | 31 |
D:40~45 | 6 |
合计 | 56 |
所以答案是:4,6;
⑶获奖年龄在30~35岁的人数约占获奖总人数百分比为 ![]() ×100%≈26.8%;
×100%≈26.8%;
C组所在扇形对应的圆心角度数约为 ![]() ×360°≈199°,
×360°≈199°,
所以答案是:26.8,199.
【考点精析】本题主要考查了频数分布直方图和扇形统计图的相关知识点,需要掌握特点:①易于显示各组的频数分布情况;②易于显示各组的频数差别.(注意区分条形统计图与频数分布直方图);能清楚地表示出各部分在总体中所占的百分比.但是不能清楚地表示出每个项目的具体数目以及事物的变化情况才能正确解答此题.


科目:初中数学 来源: 题型:
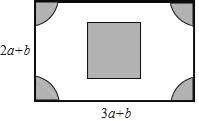
【题目】如图,有一块长(3a+b)米,宽(2a+b)米的长方形广场,园林部门要对阴影区域进行绿化,空白区域进行广场硬化,其中,四个角部分是半径为(a﹣b)米的四个大小相同的扇形,中间部分是边长为(a+b)米的正方形.
(1)用含a、b的式子表示需要硬化部分的面积;
(2)若a=30,b=10,求出硬化部分的面积(结果保留π的形式).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义:有一组邻边相等的凸四边形叫做“等邻边四边形”,在Rt△ABC中,∠ACB=90°,AB=4,AC=2,D是BC的中点,点M是AB边上一点,当四边形ACDM是“等邻边四边形”时,BM的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习一元一次方程的解法时,我们经常遇到这样的试题:
“解方程:![]() ”,请根据解题过程,在后面的括号内写出变形依据.
”,请根据解题过程,在后面的括号内写出变形依据.
解:去分母,得 ( )
去括号,得 ( )
移项,得 ( )
合并,得 (合并同类项法则)
系数化为 1,得 ( )
请你写出在进行运算时容易出错的地方(至少写出三个).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】仅用无刻度的直尺,按要求画图(保留画图痕迹,不写作法)
(1)如图①,画出⊙O的一个内接矩形; 
(2)如图②,AB是⊙O的直径,CD是弦,且AB∥CD,画出⊙O的内接正方形. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点E在AC上,∠AEB=∠ABC.
(1)图1中,作∠BAC的角平分线AD,分别交CB、BE于D、F两点,求证:∠EFD=∠ADC;
(2)图2中,作△ABC的外角∠BAG的角平分线AD,分别交CB、BE的延长线于D、F两点,试探究(1)中结论是否仍成立?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,学校有一个长方形广场,在广场的中央设计一个圆形花坛,四角都设计四分之一圆形的花坛.若长方形的长为am,宽为bm,中央圆形的半径和四个四分之一圆形的半径都为rm.
(1)列式表示广场空地的面积;(不写过程,直接写出答案)
(2)学校准备在广场四周种树,七年级四个班的学生在植树节当天进行义务植树,一班植树 x棵,二班植树的棵数比一班的多10棵,三班植树的棵数比二班的2倍少30棵,四班植树的棵数比三班的一半多20棵,求四个班一共植树多少棵?(用含x的式子表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=90°,∠AOC为∠AOB外的一个锐角,且∠AOC=30°,射线OM平分∠BOC,ON平分∠AOC.
(1)求∠MON的度数;
(2)如果(1)中∠AOB=α,其他条件不变,求∠MON的度数;
(3)如果(1)中∠AOC=β(β为锐角),其他条件不变,求∠MON的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人进行摸牌游戏.现有三张形状大小完全相同的牌,正面分别标有数字2,3,5.将三张牌背面朝上,洗匀后放在桌子上.甲从中随机抽取一张牌,记录数字后放回洗匀,乙再随机抽取一张.
(1)请用列表法或画树状图的方法,求两人抽取相同数字的概率;
(2)若两人抽取的数字和为2的倍数,则甲获胜;若抽取的数字和为5的倍数,则乙获胜.这个游戏公平吗?请用概率的知识加以解释.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com