
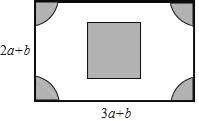
【题目】如图,有一块长(3a+b)米,宽(2a+b)米的长方形广场,园林部门要对阴影区域进行绿化,空白区域进行广场硬化,其中,四个角部分是半径为(a﹣b)米的四个大小相同的扇形,中间部分是边长为(a+b)米的正方形.
(1)用含a、b的式子表示需要硬化部分的面积;
(2)若a=30,b=10,求出硬化部分的面积(结果保留π的形式).
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:
【题目】(1)如图1,已知线段AB,点C分线段AB为5∶7,点D分线段AB为5∶11,若AB=96cm,求线段CD的长。
(2)如图2,已知线段AB上有C、D两点,AC=![]() BC,AD=
BC,AD=![]() BD,CD=14cm,求线段AB的长。
BD,CD=14cm,求线段AB的长。
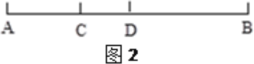
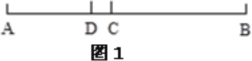
查看答案和解析>>
科目:初中数学 来源: 题型:
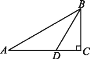
【题目】如图,在Rt△ABC中,∠C=90°,∠A=30°,BD是∠ABC的平分线,AD=20,则BC的长是 ( )
A. 20 B. 20![]() C. 30 D. 10
C. 30 D. 10![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】火车站、机场、邮局等场所都有为旅客提供打包服务的项目.现有一个长、宽、高分别为a、b 、30的箱子(其中a>b),准备采用如图①、②的两种打包方式,所用打包带的总长(不计接头处的长)分别记为![]() .
.

(1)图①中打包带的总长![]() =________.
=________.
图②中打包带的总长![]() =________.
=________.
(2)试判断哪一种打包方式更节省材料,并说明理由.(提醒:先判断再说理,说理过程即为比较 ![]() 的大小.)
的大小.)
(3)若b=40且a为正整数,在数轴上表示数![]() 的两点之间有且只有19个整数点,求a 的值.
的两点之间有且只有19个整数点,求a 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着通讯技术的迅猛发展,人与人之间的沟通方式更多样、便捷.某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选一种),在全校范围内随机调查了部分学生,将统计结果绘制了如下所示两幅不完整的统计图,请结合图中所给信息,解答下列问题:
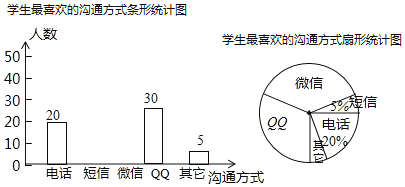
(1)本次调研活动共调研了多少名学生,表示“QQ”的扇形圆心角的度数是多少.
(2)请你补充完整条形统计图;
(3)如果该校有2000名学生,请估计该校最喜欢用“微信”进行沟通的学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是由一些棱长都为1的小正方体组合成的简单几何体.

(1)请画出这个几何体的三视图并用阴影表示出来;
(2)该几何体的表面积(含下底面)为 ;
(3)如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体的主视图和俯视图不变,那么最多可以再添加 个小正方体.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】菲尔兹奖是国际上有崇高声誉的一个数学奖项,下面的数据是从1936年至2014年菲尔兹奖得主获奖时的年龄(岁): 29 39 35 33 39 27 33 35 31 31 37 32 38 36
31 39 32 38 37 34 29 34 38 32 35 36 33 32
29 35 36 37 39 38 40 38 37 39 38 34 33 40
36 36 37 40 31 38 38 40 40 37 35 40 39 37
请根据上述数据,解答下列问题:
小彬按“组距为5”列出了如图的频数分布表
分组 | 频数 |
A:25~30 | |
B:30~35 | 15 |
C:35~40 | 31 |
D:40~45 | |
合计 | 56 |
(1)每组数据含最小值不含最大值,请将表中空缺的部分补充完整,并补全频数分布直方图; 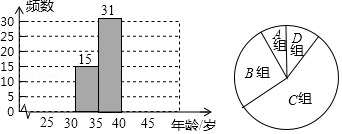
(2)根据(1)中的频数分布直方图描述这56位菲尔兹奖得主获奖时的年龄的分布特征;
(3)在(1)的基础上,小彬又画了如图所示的扇形统计图,图中获奖年龄在30~35岁的人数约占获奖总人数的%(百分号前保留1位小数);C组所在扇形对应的圆心角度数约为°(保留整数)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com