
【题目】如图,在Rt△ABC中,∠C=90°,∠A=30°,BD是∠ABC的平分线,AD=20,则BC的长是 ( )
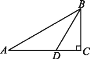
A. 20 B. 20![]() C. 30 D. 10
C. 30 D. 10![]()
科目:初中数学 来源: 题型:
【题目】下面是小丽化简的过程,仔细阅读后解答所提出的问题.
解:a(a+2b)﹣(a﹣1)2﹣2a
=a2+2ab﹣a2﹣2a﹣1﹣2a 第一步
=2ab﹣4a﹣1.第二步
(1)小丽的化简过程从第 步开始出现错误;
(2)请对原整式进行化简,并求当a=![]() ,b=﹣6时原整式的值.
,b=﹣6时原整式的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解青少年形体情况,现随机抽查了某市若干名初中学生坐姿、站姿、走姿的好坏情况.我们对测评数据作了适当处理(如果一个学生有一种以上不良姿势,以他最突出的一种作记载),并将统计结果绘制了如下两幅不完整的统计图,请你根据图中所给信息解答下列问题: 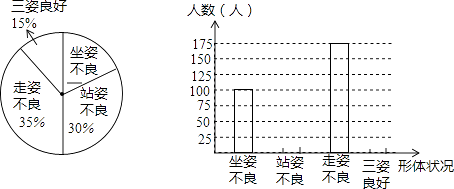
(1)请将两幅统计图补充完整;
(2)请问这次被抽查形体测评的学生一共是多少人?
(3)如果全市有5万名初中生,那么全市初中生中,坐姿和站姿不良的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△P1OA1 , △P2A1A2都是等腰直角三角形,点P1 , P2都在函数y= ![]() (x>0)的图象上,斜边OA1、A1A2都在x轴上,则点P2的坐标是( )
(x>0)的图象上,斜边OA1、A1A2都在x轴上,则点P2的坐标是( ) 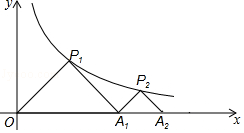
A.(4 ![]() ,
, ![]() )
)
B.(4+2 ![]() ,4﹣2
,4﹣2 ![]() )??
)??
C.(2+2 ![]() ,2
,2 ![]() ﹣2)
﹣2)
D.(4+2 ![]() ,2+2
,2+2 ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AB是直径,作OD∥BC与过点A的切线交于点D,连接DC并延长交AB的延长线于点E. 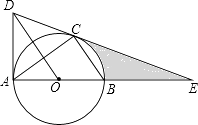
(1)判断DE与⊙O的位置关系,并证明你的结论;
(2)若AE=6,CE=2 ![]() . ①求⊙O的半径
. ①求⊙O的半径
②求线段CE,BE与劣弧 ![]() 所围成的图形的面积(结果保留根号和π)
所围成的图形的面积(结果保留根号和π)
查看答案和解析>>
科目:初中数学 来源: 题型:
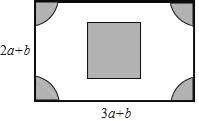
【题目】如图,有一块长(3a+b)米,宽(2a+b)米的长方形广场,园林部门要对阴影区域进行绿化,空白区域进行广场硬化,其中,四个角部分是半径为(a﹣b)米的四个大小相同的扇形,中间部分是边长为(a+b)米的正方形.
(1)用含a、b的式子表示需要硬化部分的面积;
(2)若a=30,b=10,求出硬化部分的面积(结果保留π的形式).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义:有一组邻边相等的凸四边形叫做“等邻边四边形”,在Rt△ABC中,∠ACB=90°,AB=4,AC=2,D是BC的中点,点M是AB边上一点,当四边形ACDM是“等邻边四边形”时,BM的长为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com