
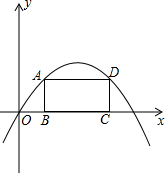
 如图,抛物线的解析式为y=-x2+6x,矩形边BC在x轴上,A,D在抛物线上(第一象限内).求矩形周长的最大值.
如图,抛物线的解析式为y=-x2+6x,矩形边BC在x轴上,A,D在抛物线上(第一象限内).求矩形周长的最大值.  天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
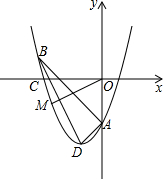 在某节习题课上,老师在黑板上写下了关于x的二次函数y=kx2+(k+1)x+2-4k.
在某节习题课上,老师在黑板上写下了关于x的二次函数y=kx2+(k+1)x+2-4k.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
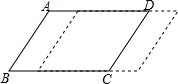 如图所示,平行四边形ABCD底边BC上的高为6cm,当边DC向右平移时,平行四边形的面积发生了变化.
如图所示,平行四边形ABCD底边BC上的高为6cm,当边DC向右平移时,平行四边形的面积发生了变化.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com