
将一张长方形的纸片 ABCD 按如图所示方式折叠,使 C 点落在 C′处,BC′交 AD 于点 E,则△EBD
的形状是 .

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
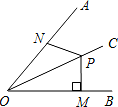
如图,OC 平分∠AOB,点 P 是 OC 上一点,PM⊥OB 于点 M,点 N 是射线 OA 上的一个动点, 若 PM=5,则 PN 的最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
学校规定学生早晨 7 时到校,小明若以每分钟 60m 的速度步行,提前 2min 到校,若以每分钟
50m 的速度步行,要迟到 2min,则小明的家到学校有 m.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com