练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    已知⊙M与⊙N的半径分别为1和5，若两圆相切，那么这两圆的圆心距MN的长等于（　　）
    A、4B、6C、4或5D、4或6
    考点：圆与圆的位置关系
    专题：
    分析：外切时，圆心距为1+5=6；内切时，圆心距5-1=4．
    解答：解：∵两圆相切，
    ∴两圆可能外切和内切，
    ∴外切时，圆心距为1+5=6；
    内切时，圆心距为5-1=4．
    ∴圆心距为6或4．
    故选D．
    点评：考查了圆与圆的位置关系，本题用到的知识点为：两圆外切，圆心距=两圆半径之和．两圆内切，圆心距=两圆半径之差．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

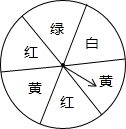    如图，有一个转盘被分成6个相同的扇形区域，颜色分别为红、黄、绿、白四中颜色，指针的位置固定，转动转盘后任其自由停止，如果指针指在等分线上，那么重新转动，直至指针指向某个扇形区域内为止，请你完成以下问题：
    ①写出两个随机事件；
    ②写出一个概率为
    1
    3
    的事件．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，水库大坝的横截面是梯形，坝顶AD宽5米，坝高10米，斜坡CD的坡角为45°，斜坡AB的坡度i=1：1.5，那么坝底BC的长度为
     
    米．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    求不等式|x-b|＞3的解集：应先求出的不等式
     
    与不等式
     
    的解集，再得不等式|x-b|＞3的解集为
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    在直角坐标系中，点M（1，-2012）关于原点的对称点坐标是（　　）
    A、（1，2012）
    B、（-1，-2012）
    C、（-1，2012）
    D、（-2012，1）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    在Rt△ABC中，已知∠ACB=90°，BC=1，AB=2，那么下列结论正确的是（　　）
    A、sinA=
    		3
    2
    B、tanA=
    1
    2
    C、cosB=
    		3
    2
    D、cotB=
    		3
    3

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （1）计算：（-
    1
    3
    ）-1-2÷
    		16
    +（3.14-π）0×cos60°；
    （2）已知x=3是关于不等式3x-
    ax+2
    2
    ＞
    2x
    3
    的解，求a的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    一名射击运动员连续打靶8次，命中的环数如图所示，这组数据的中位数是
     
    环，众数是
     
    环．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    我们定义：如果一个图形上的点A′、B′、…、P′和另一个图形上的点A、B、…、P 分别对应，并且满足：
    （1）直线AA′、BB′、…、PP′都经过同一点O；
    （2）
    OA′
    OA
    =
    OB′
    OB
    =…=
    OP′
    OP
    =k，那么这两个图形叫做位似图形，点O叫做位似中心，k叫做位似比．
    如图，在平面直角坐标系中，△ABC和△A′B′C′是以坐标原点O为位似中心的位似图形，且OB=BB′，如果点A（
    5
    2
    ，3），那么点A′的坐标为
     
    ．

    查看答案和解析>>

    同步练习册答案