
【题目】已知二次函数y=ax2+bx+3的图象分别与x轴交于点A(3,0),C(-1,0),与y轴交于点B.点D为二次函数图象的顶点.
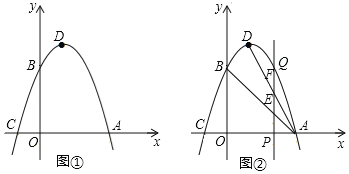
(1)如图①所示,求此二次函数的关系式:
(2)如图②所示,在x轴上取一动点P(m,0),且1<m<3,过点P作x轴的垂线分别交二次函数图象、线段AD,AB于点Q、F,E,求证:EF=EP;
(3)在图①中,若R为y轴上的一个动点,连接AR,则![]() BR+AR的最小值______(直接写出结果).
BR+AR的最小值______(直接写出结果).
【答案】(1)y=-x2+2x+3;(2)见解析;(3)![]()
【解析】
(1)根据A,C点的坐标,利用待定系数法可求出二次函数的关系式;
(2)利用待定系数法求出线段AB,AD所在直线的函数关系式,用m表示EF,EP的长,可证得结论;
(3)连接BC,过点R作RQ⊥BC,垂足为Q,则△BQR∽△AOB,利用相似三角形的性质可得出RQ=![]() BR,结合点到直线之间垂直线段最短可得出当A,R,Q共线且垂直AB时,即AR+
BR,结合点到直线之间垂直线段最短可得出当A,R,Q共线且垂直AB时,即AR+![]() BR=AQ时,其值最小,由∠ACQ=∠BCO,∠BOC=∠AQC可得出△CQA∽△COB,利用相似三角形的性质可求出AQ的值,此题得解.
BR=AQ时,其值最小,由∠ACQ=∠BCO,∠BOC=∠AQC可得出△CQA∽△COB,利用相似三角形的性质可求出AQ的值,此题得解.
解:(1)将A(3,0),C(-1,0)代入y=ax2+bx+3,得:
![]() ,解得:
,解得:![]() ,
,
∴此二次函数的关系式为y=-x2+2x+3.
(2)证明:∵y=-x2+2x+3=-(x-1)2+4,
∴点D的坐标为(1,4).
设线段AB所在直线的函数关系式为y=kx+c(k≠0),
将A(3,0),C(0,3)代入y=kx+c,得:
![]() ,解得:
,解得:![]() ,
,
∴线段AB所在直线的函数关系式为y=-x+3.
同理,可得出:线段AD所在直线的函数关系式为y=-2x+6.
∵点P的坐标为(m,0),
∴点E的坐标为(m,-m+3),点F的坐标为(m,-2m+6),
∴EP=-m+3,EF=-m+3,
∴EF=EP.
(3)如图③,连接BC,过点R作RQ⊥BC,垂足为Q.
∵OC=1,OB=3,
∴BC=![]() .(勾股定理)
.(勾股定理)
∵∠CBO=∠CBO,∠BOC=∠BQR=90°,
∴△BQR∽△AOB,
∴![]() ,即
,即![]() ,
,
∴RQ=![]() BR,
BR,
∴AR+![]() BR=AR+RQ,
BR=AR+RQ,
∴当A,R,Q共线且垂直AB时,即AR+![]() BR=AQ时,其值最小.
BR=AQ时,其值最小.
∵∠ACQ=∠BCO,∠BOC=∠AQC,
∴△CQA∽△COB,
∴![]() ,即
,即![]()
∴AQ=![]() ,
,
∴![]() BR+CR的最小值为
BR+CR的最小值为![]() .
.
故答案为:![]() .
.


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,点A、B、C的坐标分别为(﹣1,3)、(﹣4,1)、(﹣2,1),将△ABC沿一确定方向平移得到△A1B1C1,点B的对应点B1的坐标是(1,2),则点A1,C1的坐标分别是 ( )

A. A1(4,4),C1(3,2) B. A1(3,3),C1(2,1)
C. A1(4,3),C1(2,3) D. A1(3,4),C1(2,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
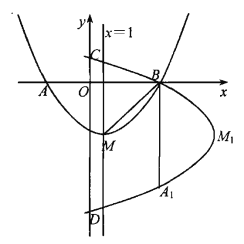
【题目】如图,抛物线y=![]() x2+bx+c的顶点为M,对称轴是直线x=1,与x轴的交点为A(-3,0)和B.将抛物线y=
x2+bx+c的顶点为M,对称轴是直线x=1,与x轴的交点为A(-3,0)和B.将抛物线y=![]() x2+bx+c绕点B逆时针方向旋转90°,点M1,A1为点M,A旋转后的对应点,旋转后的抛物线与y轴相交于C,D两点.
x2+bx+c绕点B逆时针方向旋转90°,点M1,A1为点M,A旋转后的对应点,旋转后的抛物线与y轴相交于C,D两点.
(1)写出点B的坐标及求原抛物线的解析式:
(2)求证A,M,A1三点在同一直线上:
(3)设点P是旋转后抛物线上DM1之间的一动点,是否存在一点P,使四边形PM1MD的面积最大.如果存在,请求出点P的坐标及四边形PM1MD的面积;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题9分)如图,![]() 是
是![]() 的直径,
的直径,![]() 是
是![]() 上一点,连接
上一点,连接![]() .过点
.过点![]() 作
作![]() 的切线,交
的切线,交![]() 的延长线于点
的延长线于点![]() ,在
,在![]() 上取一点
上取一点![]() ,使
,使![]() ,连接
,连接![]() ,交
,交![]() 于点
于点![]() .请补全图形并解决下面的问题:
.请补全图形并解决下面的问题:
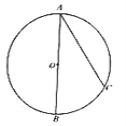
(1)求证:![]() ;
;
(2)如果![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于三角函数有如下的公式:
sin(α+β)=sinαcosβ+cosαsinβ①;cos(α+β)=cosαcosβ﹣sinαsinβ②;tan(α+β)=![]() ③
③
利用这些公式可将某些不是特殊角的三角函数转化为特殊角的三角函数来求值,
如:tan105°=tan(45°+60°)=![]() =
=![]() =
=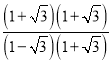 =﹣(2+
=﹣(2+![]() ).
).
根据上面的知识,你可以选择适当的公式解决下面的实际问题:
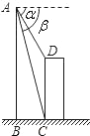
如图,直升飞机在一建筑物CD上方A点处测得建筑物顶端D点的俯角α=60°,底端C点的俯角β=75°,此时直升飞机与建筑物CD的水平距离BC为42m,求建筑物CD的高.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=2x2+4x+k﹣1.
(1)当二次函数的图象与x轴有交点时,求k的取值范围;
(2)若A(x1,0)与B(x2,0)是二次函数图象上的两个点,且当x=x1+x2时,y=﹣6,求二次函数的解析式,并在所提供的坐标系中画出大致图象;
(3)在(2)的条件下,将抛物线在x轴下方的部分沿x轴翻折,图象其余部分保持不变,得到一个新的图象,当直线y=![]() x+m(m<3)与新图象有两个公共点,且m为整数时,求m的值.
x+m(m<3)与新图象有两个公共点,且m为整数时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校初一年级68名师生参加社会实践活动,计划租车前往,租车收费标准如下:
车型 | 大巴车 (最多可坐55人) | 中巴车 (最多可坐39人) | 小巴车 (最多可坐26人) |
每车租金 (元∕天) | 900 | 800 | 550 |
则租车一天的最低费用为____元.
查看答案和解析>>
科目:初中数学 来源: 题型:
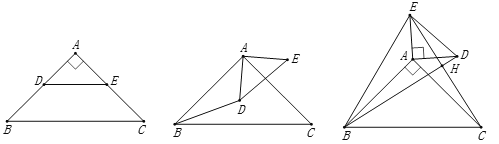
【题目】如图(1),已知点G在正方形ABCD的对角线AC上,GE⊥BC,垂足为点E,GF⊥CD,垂足为点F.
(1)证明与推断:
①求证:四边形CEGF是正方形;
②推断:![]() 的值为 :
的值为 :
(2)探究与证明:
将正方形CEGF绕点C顺时针方向旋转α角(0°<α<45°),如图(2)所示,试探究线段AG与BE之间的数量关系,并说明理由:
(3)拓展与运用:
正方形CEGF在旋转过程中,当B,E,F三点在一条直线上时,如图(3)所示,延长CG交AD于点H.若AG=6,GH=2![]() ,则BC= .
,则BC= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学课堂上,小斐同学和小可同学分别拿着一大一小两个等腰直角三角板,可分别记做![]() 和
和![]() ,其中
,其中![]() .
.
问题的产生:
两位同学先按照如图摆放,点![]() 在
在![]() 上,发现
上,发现![]() 和
和![]() 在数量和位置关系上分别满足
在数量和位置关系上分别满足![]() ,
,![]() .
.
问题的探究:
(1)将![]() 绕点
绕点![]() 逆时针旋转一定角度.如图.点
逆时针旋转一定角度.如图.点![]() 在
在![]() 内部,点
内部,点![]() 在
在![]() 外部,连结
外部,连结![]() ,上述结论依然成立吗?如果成立,请证明;如果不成立,请说明理由.
,上述结论依然成立吗?如果成立,请证明;如果不成立,请说明理由.
问题的延伸:
继续将![]() 绕点
绕点![]() 逆时针旋转.如图.点
逆时针旋转.如图.点![]() 都在
都在![]() 外部,连结
外部,连结![]() ,
,![]() ,
,![]() 与
与![]() 相交于
相交于![]() 点.
点.
(2)若![]() ,求四边形
,求四边形![]() 的面积;
的面积;
(3)若![]() ,
,![]() ,设
,设![]() ,
,![]() ,求
,求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com