
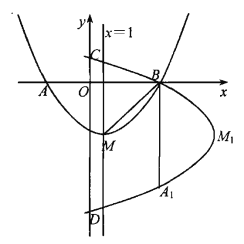
【题目】如图,抛物线y=![]() x2+bx+c的顶点为M,对称轴是直线x=1,与x轴的交点为A(-3,0)和B.将抛物线y=
x2+bx+c的顶点为M,对称轴是直线x=1,与x轴的交点为A(-3,0)和B.将抛物线y=![]() x2+bx+c绕点B逆时针方向旋转90°,点M1,A1为点M,A旋转后的对应点,旋转后的抛物线与y轴相交于C,D两点.
x2+bx+c绕点B逆时针方向旋转90°,点M1,A1为点M,A旋转后的对应点,旋转后的抛物线与y轴相交于C,D两点.
(1)写出点B的坐标及求原抛物线的解析式:
(2)求证A,M,A1三点在同一直线上:
(3)设点P是旋转后抛物线上DM1之间的一动点,是否存在一点P,使四边形PM1MD的面积最大.如果存在,请求出点P的坐标及四边形PM1MD的面积;如果不存在,请说明理由.
【答案】(1)![]() (2)见试题解析;(3)∴点P的坐标为(
(2)见试题解析;(3)∴点P的坐标为(![]() ,-7)使四边形PM1MD的面积最大,面积最大值为
,-7)使四边形PM1MD的面积最大,面积最大值为![]()
【解析】
试题(1)根据抛物线的对称性即可写出B的坐标,根据对称轴是直线x=1,与x轴的交点为A(-3,0)代入即可得到方程组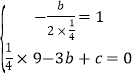 ,解方程组即可求出b、c的值,即可得到答案;
,解方程组即可求出b、c的值,即可得到答案;
(2)把x=1代入抛物线解析式即可得到M的坐标,根据旋转和图象即可求出M1、A1的坐标,设直线AM的表达式为y=kx+m,把A、M的坐标代入即可求出直线AM的解析式,根据以此函数图象上点的坐标特征确定点A1在直线AM上即可得到结论;
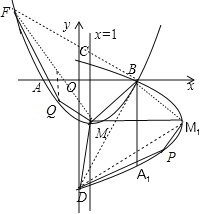
(3)连接M1D,如图,由于S△M1MD是定值,则要使四边形PM1MD的面积最大,只要S△M1PD最大,将△M1PD绕点B顺时针旋转90°,则点M1与点M重合,点P与点Q重合,点D与点F重合,利用旋转变换得点F的坐标为(-5,5),设点Q的坐标为(m,![]() ),易得直线MF的表达式为y=
),易得直线MF的表达式为y=![]() ,则根据三角形面积公式得到S△PDM1=S△QMF=
,则根据三角形面积公式得到S△PDM1=S△QMF=![]() (
(![]() -
-![]() )×(5+1)=
)×(5+1)=![]() ,根据二次函数的性质得当m=-2时,当m=-2时,S△M1PD最大=
,根据二次函数的性质得当m=-2时,当m=-2时,S△M1PD最大=![]() ,则点Q(-2,-
,则点Q(-2,-![]() ),利用旋转变换得点P的坐标为(
),利用旋转变换得点P的坐标为(![]() ,-7),然后计算S△DM1M的面积=24,再计算出四边形PM1MD的面积为24+
,-7),然后计算S△DM1M的面积=24,再计算出四边形PM1MD的面积为24+![]() =
=![]() .
.
试题(1)解:∵点B与点A(-3,0)关于直线x=1对称,
∴点B的坐标为(5,0),与x轴的交点为A(-3,0)代入即可得到方程组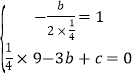 ,解得
,解得![]() ;
;
(2)点M1的坐标为(9,-4),点A1的坐标为(5,-8),设直线AM的表达式为y=kx+m,把A(-3,0),M(1,-4)代入解得,直线AM的解析式为y=-x-3,当x=5代入y=-x-3=-8,∴点A1在直线AM上,∴∠AMA1=180°;
(3)解:存在点P使四边形PM1MD的面积最大.
连接M1D,如图,∵S△M1MD是定值,∴要使四边形PM1MD的面积最大,只要S△M1PD最大,将△M1PD绕点B顺时针旋转90°,则点M1与点M重合,点P与点Q重合,点D与点F重合,则点Q,F都在抛物线y=![]() 上,由于F点的纵坐标为5,当y=5时,解得x1=-5,x2=7(舍去),∴点F的坐标为(-5,5),设点Q的坐标为(m,
上,由于F点的纵坐标为5,当y=5时,解得x1=-5,x2=7(舍去),∴点F的坐标为(-5,5),设点Q的坐标为(m,![]() )易得直线MF的表达式为y=
)易得直线MF的表达式为y=![]()
∴S△PDM1=S△QMF=![]() =
=![]()
当m=-2时,S△M1PD最大=![]() ∴点Q(-2,
∴点Q(-2,![]() ∴点P的坐标为(
∴点P的坐标为(![]() ,-7),
,-7),
∵点M的坐标为(1,-4),点M1的坐标为(9,-4),D(0,-10),
∴S△DM1M的面积=24,∴四边形PM1MD的面积为24+![]() =
=![]() ,∴点P的坐标为(
,∴点P的坐标为(![]() ,-7)使四边形PM1MD的面积最大,面积最大值为
,-7)使四边形PM1MD的面积最大,面积最大值为![]() .
.


 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
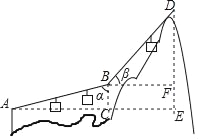
【题目】如图,游客在点A处坐缆车出发,沿A﹣B﹣D的路线可至山顶D处.已知AB=BD=800米,∠α=75°,∠β=45°,求山高DE(结果精确到1米).(参考数据:sin75°=0.966,cos75°=0.259,tan75°=3.732,![]() =1.414)
=1.414)
查看答案和解析>>
科目:初中数学 来源: 题型:
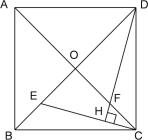
【题目】已知:如图,菱形ABCD的对角线AC与BD相交于点O,若∠CAD=∠DBC.
(1)求证:ABCD是正方形.
(2)E是OB上一点,DH⊥CE,垂足为H,DH与OC相交于点F,求证:OE=OF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+4与x轴交于A,B两点,与y轴交于点C,已知点A(-2,0),B(8,0),连接AC,BC.
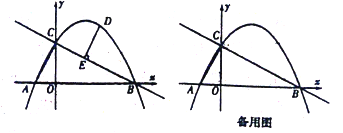
(1)求抛物线的解析式和点C的坐标;
(2)点D是直线BC上方抛物线上的一点,过点D作DE⊥BC,垂足为E,求线段DE的长度最大时,点D的坐标;
(3)抛物线上是否存在一点P(异于点A,B,C),使![]() ?若存在,请直接写出点P的坐标;若不存在,请说明理由.
?若存在,请直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
在复习《反比例函数》一课时,同桌的小明和小芳有一个间题观点不一致,小明认为如果两次分别从l到6六个整数中任取一个数,第一个数作为点![]() 的横坐标,第二个数作为点
的横坐标,第二个数作为点![]() 的纵坐标,则点
的纵坐标,则点![]() 在反比例函数
在反比例函数![]() 的的图象上的概率一定大于在反比例函数
的的图象上的概率一定大于在反比例函数![]() 的图象上的概率,而小芳却认为两者的概率相同.你赞成谁的观点?
的图象上的概率,而小芳却认为两者的概率相同.你赞成谁的观点?
(1)试用列表或画树状图的方法列举出所有点![]() 的情形;
的情形;
(2)分别求出点![]() 在两个反比例函数的图象上的概率,并说明谁的观点正确.
在两个反比例函数的图象上的概率,并说明谁的观点正确.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,BC=2AB,E,F分别是BC,AD的中点,AE,BF交于点O,连接EF,OC.
(1)求证:四边形ABEF是菱形;(2)若BC=8,∠ABC=60°,求OC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
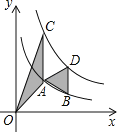
【题目】如图,点A,B在反比例函数y=![]() (x>0)的图象上,点C,D在反比例函数y=
(x>0)的图象上,点C,D在反比例函数y=![]() (k>0)的图象上,AC∥BD∥y轴,已知点A,B的横坐标分别为1,2,△OAC与△ABD的面积之和为
(k>0)的图象上,AC∥BD∥y轴,已知点A,B的横坐标分别为1,2,△OAC与△ABD的面积之和为![]() ,则k的值为_____.
,则k的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+3的图象分别与x轴交于点A(3,0),C(-1,0),与y轴交于点B.点D为二次函数图象的顶点.
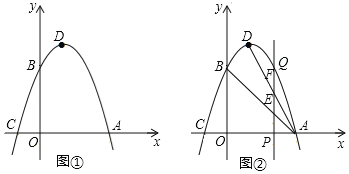
(1)如图①所示,求此二次函数的关系式:
(2)如图②所示,在x轴上取一动点P(m,0),且1<m<3,过点P作x轴的垂线分别交二次函数图象、线段AD,AB于点Q、F,E,求证:EF=EP;
(3)在图①中,若R为y轴上的一个动点,连接AR,则![]() BR+AR的最小值______(直接写出结果).
BR+AR的最小值______(直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙3人聚会,每人带了一件礼物,3件礼物从外盒包装看完全相同,里面的东西只有颜色不同,将3件礼物放在一起.
(1)甲从中随机抽取一件,求甲抽到不是自己带来的礼物的概率;
(2)每人从中随机抽取一件,求甲、乙、丙3人抽到的都不是自己带来的礼物的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com