
【题目】如图,已知在△ABC中,AB=AC,∠BAC=120°.
(1)用尺规作AC的垂直平分线EF交AC于点E,交BC于点F.(不写作法,但保留作图痕迹)
(2)求证:BF=2CF.
【答案】(1)详见解析;(2)详见解析
【解析】
(1)利用基本作图(作已知线段的垂直平分线)作出EF垂直平分AC即可;
(2)连接AF,先利用等腰三角形的性质和三角形内角和计算出∠B=∠C=30°,再根据线段垂直平分线的性质得AF=FC,则∠FAC=∠C=30°,接着计算出∠BAF=90°,利用含30°的直角三角形的性质得到2AF=BF,从而得到结论.
(1)解:如图,EF即为所作;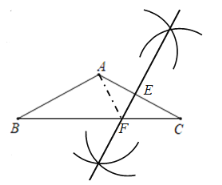
(2)证明:连接AF,
∵AB=AC,
∴∠B=∠C=![]() (180°-∠BAC)=
(180°-∠BAC)=![]() (180°-120°)=30°,
(180°-120°)=30°,
∵EF垂直平分AC,
∴AF=FC,
∴∠FAC=∠C=30°,
∴∠BAF=120°-30°=90°,
在Rt△ABF中,AF=![]() BF,
BF,
∴CF=![]() BF,
BF,
∴BF=2CF.


 新思维寒假作业系列答案
新思维寒假作业系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,函数
中,函数![]() 的图象与直线
的图象与直线![]() 交于点A(3,m).
交于点A(3,m).
(1)求k、m的值;
(2)已知点P(n,n)(n>0),过点P作平行于![]() 轴的直线,交直线y=x-2于点M,过点P作平行于y轴的直线,交函数
轴的直线,交直线y=x-2于点M,过点P作平行于y轴的直线,交函数![]() 的图象于点N.
的图象于点N.
①当n=1时,判断线段PM与PN的数量关系,并说明理由;
②若PN≥PM,结合函数的图象,直接写出n的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在每个小正方形的边长为1的网格图形中,每个小正方形的顶点称为格点.如图,5×5正方形方格纸图中,点A,B都在格点处.
(1)请在图中作等腰△ABC,使其底边AC=2![]() ,且点C为格点;
,且点C为格点;
(2)在(1)的条件下,作出平行四边形ABDC,且D为格点,并直接写出平行四边形ABDC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请根据图中提供的信息,回答下列问题

(1)一个暖瓶与一个水杯分别是多少元?
(2)甲、乙两家商场同时出售同样的暖瓶和水杯,为了迎接新年,两家商场都在搞促销活动,甲商场规定: 这两种商品都打九折;乙商场规定:买一个暖瓶赠送一个水杯。若某单位想要买4个暖瓶和15个水杯,请问选择哪家商场购买更合算,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法: ①2a+b=0;②当-1≤x≤3时,y<0;③若(x1 , y1)、(x2 , y2)在函数图象上,当x1<x2时,y1<y2;④9a+3b+c=0,其中正确的是( )
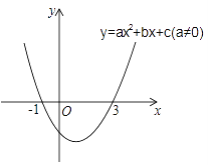
A. ①②③ B. ①②④ C. ①④ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
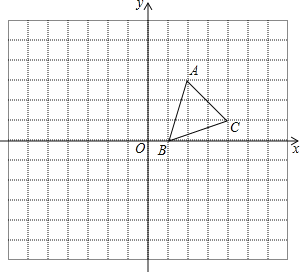
【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,![]() 的顶点均在格点上,点
的顶点均在格点上,点![]() 坐标为
坐标为![]() .
.
(1)画出![]() 关于
关于![]() 轴对称的
轴对称的![]() ;
;
(2)画出将![]() 绕原点
绕原点![]() 逆时针旋转90°所得的
逆时针旋转90°所得的![]() ;
;
(3)![]() 与
与![]() 能组成轴对称图形吗?若能,请你画出所有的对称轴.
能组成轴对称图形吗?若能,请你画出所有的对称轴.
查看答案和解析>>
科目:初中数学 来源: 题型:
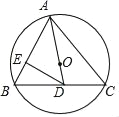
【题目】如图,已知锐角△ABC内接于⊙O,连接AO并延长交BC于点D.
(1)求证:∠ACB+∠BAD=90°;
(2)过点D作DE⊥AB于E,若∠ADC=2∠ACB,AC=4,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】第二十四届冬季奥林匹克运动会将于2022年在北京市和张家口市举行.为了调查学生对冬奥知识的了解情况,从甲、乙两校各随机抽取20名学生进行了相关知识测试,获得了他们的成绩(百分制),并对数据(成绩)进行了整理、描述和分析.下面给出了部分信息.
a.甲校20名学生成绩的频数分布表和频数分布直方图如下:
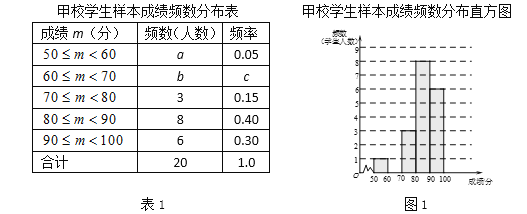
b.甲校成绩在![]() 的这一组的具体成绩是:
的这一组的具体成绩是:
87 88 88 88 89 89 89 89
c.甲、乙两校成绩的平均分、中位数、众数、方差如下:
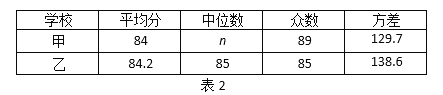
根据以上图表提供的信息,解答下列问题:
(1)表1中a = ;表2中的中位数n = ;
(2)补全图1甲校学生样本成绩频数分布直方图;
(3)在此次测试中,某学生的成绩是87分,在他所属学校排在前10名,由表中数据可知该学生是 校的学生(填“甲”或“乙”),理由是 ;
(4)假设甲校200名学生都参加此次测试,若成绩80分及以上为优秀,估计成绩优秀的学生人数为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com