
��ͼ���ȱ�������ABC�ı߳�Ϊ6cm������P�ӵ�A������2cm/����ٶ���AC�������յ�C�˶���ͬʱ����Q�ӵ�C������1cm/����ٶ���CB�������յ�B�˶�������P��Q�ֱ�����AB�Ĵ��߶�PM��PN������ֱ�Ϊ��M��N����P��Q�����˶�ʱ��Ϊt�루0��t��3�����ı���MNQP�����ΪS cm2��
��1���ڵ�P��Q���˶��Ĺ����У�tΪ��ֵʱ��PQ��AB��
��2�����ı���MNQP�����S���˶�ʱ��t�仯�ĺ�����ϵʽ��
��3���Ƿ����ijһʱ��t��ʹ�ı���MNQP�����S���ڡ�ABC�������
 �������ڣ������ʱt��ֵ���������ڣ�˵�����ɣ�
�������ڣ������ʱt��ֵ���������ڣ�˵�����ɣ�


�����㡿�������ۺ��⣮
����������1����PQ��ABʱ���ɡ�ABC�ǵȱ������Σ��ó���PQC�ǵȱ������Σ�PC=QC���ó�����6��2t=t���ⷽ�̼��ɣ���2����APM�͡�BQN������һ������60���ֱ�������Σ����ݹ��ɶ����ɷֱ����AM��PM��BN��QN��Ȼ�����ֱ�����εĸ�MN�������������ʽ����ı���MNQP�����S���˶�ʱ��t�仯�ĺ�����ϵʽ��
��3�����������г����̼��ɽ��t��ֵ��Ȼ���Ƿ�����0��t��4��
����𡿽⣺��1��t=2sʱ��PQ��AB���������£�
��PQ��ABʱ���ߡ�ABC�ǵȱ������Σ�
���PQC�ǵȱ������Σ�
��PC=QC��
��6��2t=t��
��ã�t=2��
��t=2sʱ��PQ��AB��
��2����������ã�AP=2t��QB=8��t����APM�͡�QNB��ֱ�������Σ��ı���MNQP��ֱ�����Σ�
��Rt��APM��Rt��QNB��AM=
 AP=t��PM=
AP=t��PM=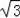
 t��BN=
t��BN=
 ��6��t����QN=
��6��t����QN=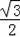
 ��6��t����
��6��t����
��MN=AB��AM��BN=6��t��
 ��6��t��=3��
��6��t��=3��
 t��
t��
��S=
 ��PM+QN��•MN=
��PM+QN��•MN=
 [
[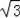
 t+
t+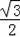
 ��6��t��]•��3
��6��t��]•��3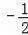
 t��=��
t��=��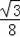
 t2+
t2+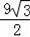
 ��
��
��S=��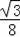
 t2+
t2+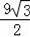
 ��
��
��3���������ijһʱ��t��ʹ�ı���MNQP�����S���ڡ�ABC�������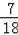
 ��
��
��S=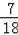
 S��ABC��
S��ABC��
��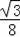
 t2+
t2+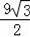
 =
=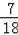
 ��
��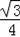
 ��62��
��62��
�����ã�t2=8��
��ã�t=��2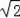
 ����ֵ��ȥ����
����ֵ��ȥ����
��t=2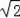
 sʱ���ı���MNQP�����S���ڡ�ABC�������
sʱ���ı���MNQP�����S���ڡ�ABC�������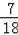
 ��
��
���������������������ۺ��⣬�������������ε����ʺ�ֱ�������ε����ʡ������κ���������ļ��㡢��������ʽ�����Լ����̵�֪ʶ�������ѶȽϴ��ۺ���ǿ���Ѻ���������ں���һ�𣬱Ƚϸ��ӣ����ѧ���ļ���������


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
ѧУ�̵���һ��ʱ�����������������Ϲ�100ƿ���������ϵ����������±���
| Ʒ�� | �� | �� | �� | �� |
| ��������ƿ�� | 12 | 32 | 13 | 43 |
����ѧУ�̵������������Ʒ���ǣ� ��
A.��Ʒ�� B.��Ʒ�� C.��Ʒ��  D.��Ʒ��
D.��Ʒ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
ijУ�Ӽס�������ѡ����ѡһ���μ����˶�����ᄊ���ױ���������Ա������ѡ��ͬʱ����8�Σ�������£�����λ���룩
�ף�12.1��12.2��13��12.5��13.1��12.5��12.4��12.2
�ң�12��12.4��12.8��13��12.2��12.8��12.3��12.5
���ݲ��Գɼ�����������ѧ����ͳ��֪ʶ�� ������һλ���ã�Ϊʲô��
������һλ���ã�Ϊʲô��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
С������һ������y=
 ��ͼ����ͼ����ô����x�ķ�ʽ����
��ͼ����ͼ����ô����x�ķ�ʽ����
 =2�Ľ��ǣ�������
=2�Ľ��ǣ�������


A��x=1 B��x=2 C��x=3 D��x=4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
���㣺����2a��2•����3a��3�Ľ���ǣ�������
A����108a5 B����108a6 C��108a5 D��108a6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
ijѧ��7��ѧ�ƿ��Գɼ����ܷ���560�֣�����3��ѧ�Ƶ��ܷ���234�֣�������4��ѧ�Ƴɼ���ƽ������_________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��֪ƽ���ı���ABCD���ܳ�Ϊ32��AB=4����BC�ij�Ϊ�� ��
A��4 B��12 C��24 D��28
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ���ܳ�Ϊ16������ABCD�У���E��F�ֱ���AB��AD���ϣ�AE=1��AF=3��PΪBD��һ���㣬���߶�EP+FP�ij����Ϊ�� ��
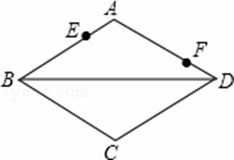
A��3 B��4 C��5 D��6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�ڣ�1�� ����2��
����2�� ����3��
����3�� ��������ֵ�У�_____�Ƿ�����x��3y��9�Ľ⣬______�Ƿ���2 x��y��4�Ľ⣬______�Ƿ�����
��������ֵ�У�_____�Ƿ�����x��3y��9�Ľ⣬______�Ƿ���2 x��y��4�Ľ⣬______�Ƿ����� �Ľ⣮
�Ľ⣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com