
 如图,点C坐标为(2,0),∠ACO=90°,∠AOC=60°,双曲线y=$\frac{k}{x}$在第一象限内的图象经过OA边的中点B,则k=$\sqrt{3}$.
如图,点C坐标为(2,0),∠ACO=90°,∠AOC=60°,双曲线y=$\frac{k}{x}$在第一象限内的图象经过OA边的中点B,则k=$\sqrt{3}$. 科目:初中数学 来源: 题型:选择题
| A. | x2+y2+2x+2y | B. | x2+y2+2xy-2 | C. | x2-y2+4x+4y | D. | x2-y2+4y-4 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 种子粒数 | 100 | 400 | 800 | 1000 | 2000 | 5000 |
| 发芽种子粒数 | 85 | 298 | 652 | 793 | 1604 | 4005 |
| 发芽种子频率 | 0.850 | 0.745 | 0.815 | 0.793 | 0.802 | 0.801 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,抛物线y=$\frac{1}{3}$x2+bx-1与x轴分别相交于点A、B,与y轴相交于点C,且OA=OC.
如图,抛物线y=$\frac{1}{3}$x2+bx-1与x轴分别相交于点A、B,与y轴相交于点C,且OA=OC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=2(x+3)2+3 | B. | y=2(x-3)2+3 | C. | y=2(x+3)2-1 | D. | y=2(x-3)2-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 星期天早晨,小明骑自行车从家里到植物园,途中到早餐店吃饭花了一段时间,然后继续骑行,直至到达植物园(假设在骑自行车过程中匀速行驶).
星期天早晨,小明骑自行车从家里到植物园,途中到早餐店吃饭花了一段时间,然后继续骑行,直至到达植物园(假设在骑自行车过程中匀速行驶).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
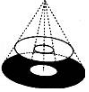 圆桌面(桌面中间有一个直径为0.4m的圆洞)正上方的灯泡(看作一个点)发出的光线照射平行于地面的桌面后,在地面上形成如图所示的圆环形阴影.已知桌面直径为1.2m,桌面离地面1m,若灯泡离地面3m,则地面圆环形阴影的面积是( )
圆桌面(桌面中间有一个直径为0.4m的圆洞)正上方的灯泡(看作一个点)发出的光线照射平行于地面的桌面后,在地面上形成如图所示的圆环形阴影.已知桌面直径为1.2m,桌面离地面1m,若灯泡离地面3m,则地面圆环形阴影的面积是( )| A. | 0.324π m2 | B. | 0.288π m2 | C. | 1.08π m2 | D. | 0.72π m2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com